基本介紹
- 中文名:緊化
- 外文名:compactification
- 又稱:緊緻化
- 學科:物理學
- 套用:弦理論
歷史
簡介
場論中的緊緻化
弦論中的緊緻化





擴展:緊化(數學)


亞歷山德羅夫單點緊化




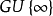
















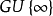





在物理學中,緊緻(compactification),又稱緊緻化,指改變時空中某些維度的拓撲結構,使其從展開的無限大尺度,變成有限大的周期性結構。緊化在弦理論中用於解決多維空間...
單點緊化(one-point compactification)亦稱亞歷山德羅夫緊化,是一種特殊的緊化。將拓撲空間嵌入緊空間的一種方式。設(X,J)是拓撲空間,∞是一個抽象的點,令X*...
緊化維數(dimension of compactification)關於維數的一組定理:若月X為X的斯通一切赫緊化,則有下述結果: 1.當X為T。空間時,Ind月X=IndX. 2.當X為吉洪諾夫...
完全緊化(perfect compactification)一類特殊的緊化.設aX為完全正則空間X的緊化,8為aX上的一個鄰近.若對於X的任意開集U與任意ACL,',有A}(X -U),若且唯若...
極大緊化(maximal compactification)一種特殊的緊化.設X為吉洪諾夫空間,}(X)表示X的所有T:緊化的族,又設:1(X)與:z (X)為X的兩個},:緊化.若存在連續...
δ緊化(δ-compactification)亦稱斯米爾諾夫緊化一種特殊的緊化.對於鄰近空間X,惟一地存在X的緊化u(X),使得X鄰近同構於u(X)的一個稠密子空間.這時u(X)稱為...
瓦勒曼緊化(Wallman compactification)一種特殊的緊化.對於每個T,空間X,可構造一個以X為稠密子空間的緊T:空間wX,使得對於任意緊T:空間Z與任意連續映射f : X-...
維度減化(英語:Dimensional reduction)是緊化理論中緊緻化的維度的大小變為零時的臨界情況。在物理學中,通過將所有的場獨立存在於額外維度D中,時空維數D的理論...
