基本介紹
- 中文名:單點緊化
- 外文名:one-point compactification
- 所屬學科:數學
- 所屬領域:拓撲學
- 別名:亞歷山德羅夫緊化
基本概念,相關性質,定理1,定理2,定理3,定理4,
基本概念
定義1 一個拓撲空間是局部緊緻的,如果對於任一 ,存在一個包含於X的一個緊緻子集之中的鄰域。
,存在一個包含於X的一個緊緻子集之中的鄰域。

例1任一緊緻空間當然是局部緊緻的,由於每一個 都有既作為它的一個鄰域又作為包含此鄰域的一個緊緻集的X。
都有既作為它的一個鄰域又作為包含此鄰域的一個緊緻集的X。

例2實軸R是局部緊緻的,由於對於任一 ,我們有
,我們有 而
而 是緊緻的。
是緊緻的。



例3R的在標準拓撲中的子空間Q不是局部緊緻的。
(1)在X中是開集;
(2)形如 的集合,其中C是X的一個緊緻子集。
的集合,其中C是X的一個緊緻子集。

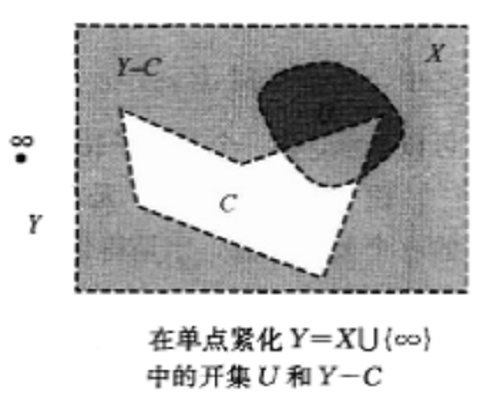
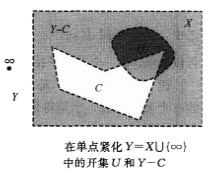 圖1
圖1我們稱所得到的拓撲空間Y為X的單點緊化。
相關性質
當然,我們需要證實,此開集族所描述的恰好是一個拓撲,下面進行證實。
定理1
證明: 空集是Y中的開集,由於它是X中的一個開子集。整個集合Y本身,在Y中也是開集,由於它在Y中是空集 的補集,而
的補集,而 是X的一個緊緻子集。
是X的一個緊緻子集。


為了證明Y中開集的有限交在Y中是開集,只要檢驗一對開集U與V的交就可以了,然後再用數學歸納法,就可以得到任意有限交的結果了。為此,設U與V是Y中的開集。我們需要檢驗3種不同的情況,首先,如果U與V都是X中的開集,那么 是X中的一個開集,從而使它成為Y中的一個開集。其次,假定
是X中的一個開集,從而使它成為Y中的一個開集。其次,假定 與
與 ,其中
,其中 是X的緊緻子集。於是
是X的緊緻子集。於是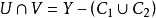 。由於緊緻集的有限並仍是緊緻的,因此
。由於緊緻集的有限並仍是緊緻的,因此 是X的一個緊緻子集。於是得出,對於X的一個緊緻子集C,
是X的一個緊緻子集。於是得出,對於X的一個緊緻子集C, 因而在這種情況下,
因而在這種情況下, 在Y中同樣是開集。最後,假定U是X中的開集,而
在Y中同樣是開集。最後,假定U是X中的開集,而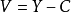 ,其中C是X的一個緊緻子集。那么,由於
,其中C是X的一個緊緻子集。那么,由於 不在U中,於是得出
不在U中,於是得出 。而C在X中是閉的,由於它在豪斯多夫空間X中是一個緊緻集,因此,
。而C在X中是閉的,由於它在豪斯多夫空間X中是一個緊緻集,因此, 在X中是開的,蘊涵
在X中是開的,蘊涵 在X中為開。於是
在X中為開。於是 在X中為開,從而在此時使得它在Y中也為開。於是得出,如果U與V是Y中的任意開集,那么
在X中為開,從而在此時使得它在Y中也為開。於是得出,如果U與V是Y中的任意開集,那么 在Y中也是開的,這正是我們所要證明的。
在Y中也是開的,這正是我們所要證明的。




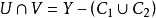



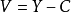






最後,我們證明開集的任意並是開集,我們可以把這一任意並表示為以下的形式:
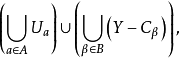



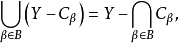












X是單點緊化 的一個子集,因此,X從Y傳承一個子空間拓撲,以下的定理指出這個子空間拓撲與原拓撲是相同的,因而我們可以把X看作是它的單點緊化的一個子空間。
的一個子集,因此,X從Y傳承一個子空間拓撲,以下的定理指出這個子空間拓撲與原拓撲是相同的,因而我們可以把X看作是它的單點緊化的一個子空間。

定理2
設X是一個豪斯多夫空間,並設 是它的單點緊化,那么傳承自Y的X的子空間拓撲,等於X上的原拓撲。
是它的單點緊化,那么傳承自Y的X的子空間拓撲,等於X上的原拓撲。

接下來,我們說明使用術語“緊緻化”的理由。
定理3
設X是一個豪斯多夫空間,它的單點緊化, 是緊緻的。
是緊緻的。

定理4
設X是一個局部緊緻的豪斯多夫空間,那么,X的單點緊化 是豪斯多夫的。
是豪斯多夫的。

證明:為了看出Y是豪斯多夫的,設x與y是Y中的點。在第一種情況下,假定x與y都在X中,由於X是豪斯多夫空間,我們就可以在X中找到分別包含x與y的分離開集U與V,集合U與V在Y中也是開集,因而在Y中存在x與y的分離鄰域。在第二種情況下,設 且
且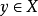 。由於X是局部緊緻的,因此在包含y的一個鄰域U的X中,存在一個緊緻子集C。Y中的開集
。由於X是局部緊緻的,因此在包含y的一個鄰域U的X中,存在一個緊緻子集C。Y中的開集 和U是分離集,且分別包含x與y。於是在這種情況下,在Y中也存在x與y的分離鄰域,因此,Y是豪斯多夫的。
和U是分離集,且分別包含x與y。於是在這種情況下,在Y中也存在x與y的分離鄰域,因此,Y是豪斯多夫的。