基本介紹
方程的敘述
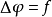
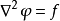



數學表達
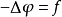
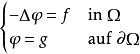
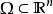
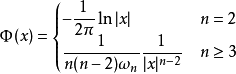
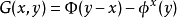





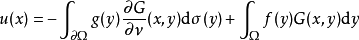
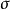

套用
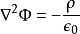
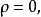
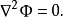






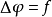
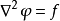



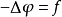
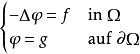
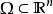
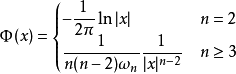
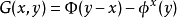





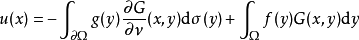
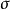

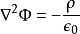
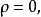
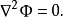





泊松方程是數學中一個常見於靜電學、機械工程和理論物理的偏微分方程。是因法國數學家、幾何學家及物理學家泊松而得名的。泊松首先在無引力源的情況下得到泊松方程...
勢函式的一種二階偏微分方程。廣泛套用於電學、磁學、力學、熱學等多種熱場的研究與計算。...
泊松-玻爾茲曼方程 (英語:Poisson- Boltzmann Equation)是用來計算電解質溶液中離子濃度和電荷密度分布的一個微分方程。...
泊松方程是數學中一個常見於靜電學、機械工程和理論物理的偏微分方程。是從法國數學家、幾何學家及物理學家泊松而得名的。...
西莫恩·德尼·泊松(Simeon-Denis Poisson 1781~1840)法國數學家、幾何學家和物理學家。1781年6月21日生於法國盧瓦雷省的皮蒂維耶,1840年4月25日卒於法國索...
拉普拉斯方程(Laplace's equation)又稱調和方程、位勢方程,是一種偏微分方程,因由法國數學家拉普拉斯首先提出而得名。拉普拉斯方程表示液面曲率與液體表面壓強之間的...
玻爾茲曼方程或玻爾茲曼輸運方程(Boltzmann transport equation,BTE)是一個描述非熱力學平衡狀態的熱力學系統統計行為的偏微分方程,由路德維希·玻爾茲曼於1872年提出。...
在數學中,劉維爾方程(Liouville equation),又稱劉維 - 布拉-蓋爾芬德方程(Liouville-Bratu-Gelfand equation)是一個非線性特徵值泊松方程,以數學家約瑟夫·劉維爾(...
場方程是描述場的運動規律的方程。著名的場方程有愛因斯坦場方程等。...... 場方程對應原理 透過弱場近似以及慢速近似,可以從愛因斯坦場方程退化為泊松方程。事實上,...
漂移-擴散方程是用來描述半導體中載流子的運動規律的方程。它描述了兩類運動:擴散電流和漂移電流。漂移擴散方程和泊松方程一起可以用來計算半導體內的電勢分布和載流子...
引力場方程是指描述引力場的時空幾何量,作為引力場源的物質能量動量張量的方程。這個方程反映了愛因斯坦的馬赫原理的思想。1905年愛因斯坦發表狹義相對論後,他開始著眼...
偏微分方程論(theory of partial differential e- quations)指包含多元函式的偏導數等式的偏微分方程,描述自變數、未知函式及其偏導數之間的關係。符合這個關係的函式...
托馬斯-費米方程是計算原子中的電荷分布及電場的方程,是托馬斯-費米方法的基本方程,托馬斯-費米方法是在1927年提出的,由提出者E.Fermi(費米)和L.Thomas(托馬斯)...
萊恩-埃姆登方程是天文物理中一個表現自引力位能,球對稱多方流體的無量綱泊松方程。...
惟一性定理指出,很大一部分的具有邊界條件的泊松方程,可能有很多個解,但所有解的梯度都是相同的。...
5.4 泊松方程和準泊松方程的差分離散5.5 直流電機負載時的非線性磁場5.6 正弦渦流方程的差分離散5.7 瞬態渦流方程的差分離散小結...
6.2 泊松方程的有限元公式6.3 軸對稱場的有限元公式6.4 有限元法舉例思考題6第7章 電磁場的邊界元法7.1 一維泊松方程的邊界元法...
圓環函式(ring function or toroidal function)是圓環坐標系下求解拉普拉斯方程時出現的一類特殊函式。拉普拉斯方程是以法國數學家、天文學家P.S.拉普拉斯(Pierre Simon...
nextnano為下一代納米器件計算工具,以採用量子力學方法(薛丁格方程,泊松方程,連續電流方程),通過自洽計算研究納米半導體器件的電子和光學特性,是一個計算納米半導體的...
從變分法、微分方程、積分方程、函式論以及量子物理等的研究中發展起來的,它運用幾何學、代數學的觀點和方法研究分析學的課題,可看作無限維的分析學。...
6.求解波動方程的高精度緊緻隱式差分方法 寧夏大學學報 2005年第12期 一作 核心 7.三維泊松方程的高精度多重格線解法 套用數學 2006年第2期 一作 核心 8.含...
