場方程是描述場的運動規律的方程。著名的場方程有愛因斯坦場方程等。
基本介紹
- 中文名:場方程
- 外文名:field equations
- 定義:描述場的運動規律的方程
- 學科:物理
愛因斯坦場方程
數學形式

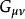

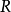



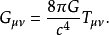

性質
能量與動量守恆
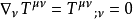
場方程為非線性的
對應原理
真空場方程
宇宙常數為零
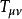
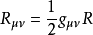
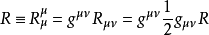


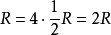

宇宙常數不為零


愛因斯坦-麥克斯韋方程

參見
- 廣義相對論資源
場方程是描述場的運動規律的方程。著名的場方程有愛因斯坦場方程等。

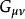

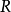



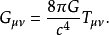

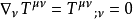
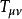
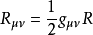
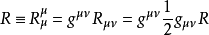


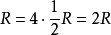




場方程是描述場的運動規律的方程。著名的場方程有愛因斯坦場方程等。...... 愛因斯坦引力場方程是一組含有十個方程的方程組,由愛因斯坦於1915年在廣義相對論中提出。...
愛因斯坦場方程是一個二階張量方程,R_uv為里契張量表示了空間的彎曲狀況。T_uv為能量-動量張量,表示了物質分布和運動狀況。...
電磁場方程組由描述巨觀電磁場現象普遍規律的方程式或方程組構成的。包括庫侖定律,麥克斯韋方程組、靜電場和恆定磁場的基本方程、無源區的波動方程等,揭示了不同條件...
圖科斯基方程(英文:Teukolsky equation)是康奈爾大學的索爾·圖科斯基(Saul Teukolsky)於二十世紀七十年代創立的克爾度規下的廣義相對論引力場方程。方程的基本思想是...
“相對論場方程”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
克萊因-戈爾登方程(Klein-Gordon equation)是相對論量子力學和量子場論中的最基本方程,它是薛丁格方程的狹義相對論形式,用於描述自旋為零的粒子。克萊因-戈爾登方程...
重力場方程式(gravitational field equations):廣義相對論的基本方程式,是一組具有十個分量的張量方程式,描述物質與能量的存在如何使時空結構彎曲,重力則隱含在彎曲的...
在物理學中,特別是相對論量子力學(RQM)及其在粒子物理學中的套用,相對論波動方程(Relativistic wave equations)預測了粒子在高能量和速度下的行為,與光速相當。在...
1917年﹐愛因斯坦利用他的引力場方程﹐ 對宇宙整體進行了考察。為了解釋物質密度不為零的靜態宇宙的存在﹐他在場方程中引進一個與度規張量成比例的項﹐用符號Λ ...
史瓦西解,是指天文學家史瓦西(舊譯席瓦希爾)求出的愛因斯坦方程的第一個嚴格解。這個解表明球外引力場只取決於引力源的總質量。亦稱史瓦西外部解...
葛墨林院士指出,越來越多的數學家參與到楊·米爾斯場方程和楊·巴斯特方程的研究工作中,同時不少前沿物理問題也和兩個問題密切相關,因此喜歡理論物理、數學物理的人...
《廣義相對論和引力場理論》是科學出版社2000-1出版的圖書。...... 主要內容有等效原理、時空曲率張量和引力場方程、坐標選擇與測量之間的關係等。廣義相對論和引力...
