基本介紹
定義,數學表達,導數與積分,級數展開式,套用,
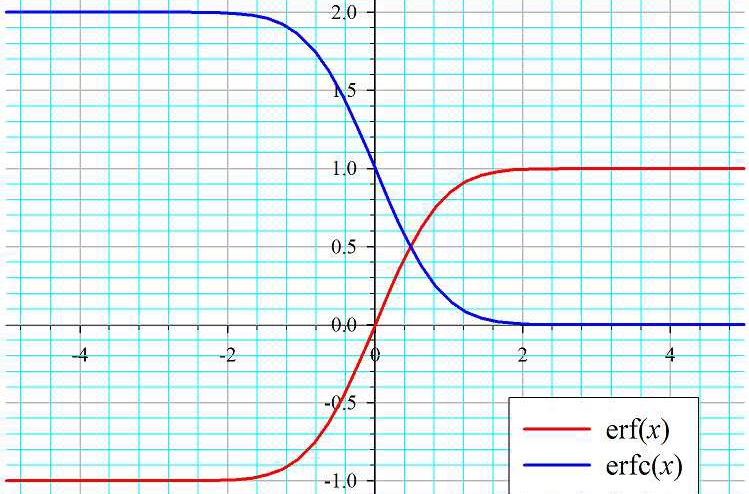
在數學中,誤差函式(也稱之為高斯誤差函式,error function or Gauss error function)是一個非基本函式(即不是初等函式),其在機率論、統計學以及偏微分方程和半導體...
高斯誤差函式,英文名Gaussian。是傅立葉變換的特徵函式。...... 高斯誤差函式,英文名Gaussian。是傅立葉變換的特徵函式。中文名 高斯誤差函式 外文名 Gaussian ...
平均絕對誤差(Mean Absolute Deviation),又叫平均絕對離差,是所有單個觀測值與算術平均值的偏差的絕對值的平均。平均絕對誤差可以避免誤差相互抵消的問題,因而可以準確...
在統計學上,由於變數含有誤差,而使函式受其影響也含有誤差,稱之為誤差傳播。闡述這種關係的定律稱為誤差傳播定律。誤差傳播定律:闡述觀測值中誤差與觀測值函式中...
Mittag-Leffler函式(米塔格-累夫勒函式)是一個特殊函式,形式見正文。...... Mittag-Leffler函式(米塔格-累夫勒函式)是一...指數函式:[1] 誤差函式[1] 雙曲餘弦函...
