物理學中的平衡態或定常態問題,例如彈性膜的平衡、彈性柱的扭轉、定常態熱傳導、電場、磁場、滲流、亞聲速流及不可壓縮無旋流等等,通常都可歸結為橢圓型偏微分方程邊值問題。
基本介紹
- 中文名:偏微分方程邊值問題差分方法
- 特點:直觀、簡易、普遍
- 典型例子:泊松方程的邊值問題
- 屬於:學術
正文
第一類:=,
第二類: 第三類: 式中表示外法嚮導數,、和是定義在嬠上的已知函式。附加第一類和第二類邊界條件的問題分別稱為狄利克雷問題和馮·諾伊曼問題;有些問題在邊界不同區段滿足不同類的邊界條件,稱為混合邊值問題。
橢圓型邊值問題的求解,只在很特殊情況下才能用解析方法,一般情況下實際有效的途徑是數值方法,差分法是其中一類。
差分法的思想和做法是,把定解區域剖分為格線,在格線結點上以差商代替微商或用某種插值方式,把微分方程化為包含有限個未知數的差分方程組。差分法直觀、簡易、能普遍用於各種類型的微分方程和任意形狀的區域。因為它包含巨大的運算量,所以只在電子計算機問世之後,才得到廣泛的套用和發展。
從微分方程出發的差分化 格線剖分的一種最簡單又常用的做法是取平行於坐標軸的直線作為格線線,例如取=,=,、為步長,、取一切整數,這時格線結點為(,)。對方程(1)進行差分化、以表示差分近似解、表示在格線結點(,)上的分量。如果(,)是內結點,即鄰近四個格線結點都在上,則用中心二階差商代替二階微商代入(1),即得相應的差分方程
 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法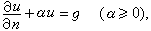 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法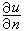 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法式中()、()取邊界值,,是線段、的長度。
對第二、第三類邊值問題,可取外最靠近嬠的一層格線結點為邊界結點,相應的差分方程可建立如下:設邊界結點及其鄰近的邊界如圖2所示,過結點作嬠的法線,它與嬠和格線線分別交於和,用差商代替的外法嚮導數,其中()利用格線結點和上的值作線性插值,即
 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法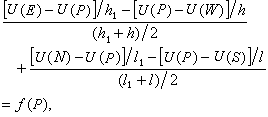 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法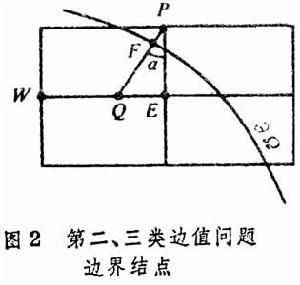 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法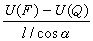 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法還可以用其他插值方法作邊界處理。但是,這種對微分方程及其邊界條件分開處理的方法,對自共軛邊值問題,包括現在討論的最簡單的典型例子,所得差分方程組的係數矩陣一般都不具有對稱性。
從積分守恆原理出發的差分化 與平衡態或定常態緊密聯繫的橢圓型邊值問題,在物理上表示某種守恆規律,在數學上表現為某種積分守恆形式。例如與方程(1)等價的積分守恆形式為
 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法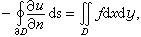 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法偏微分方程邊值問題差分方法偏微分方程邊值問題差分方法對(3)的右端,作逼近
 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法從變分原理出發的差分化 平衡態或定常態的物理問題,往往可用變分原理表達,即表示為一個極小值問題。例如微分方程(1)的第一邊值問題,就等價於泛函
 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法從變分原理出發進行差分化,其步驟是先對區域作格線剖分,然後對積分(7)或(8)進行差分逼近,得到一個有限和式,它是定義在格線結點上的差分解的二次函式,它的極小解可歸結為解線性方程組,此方程組的係數矩陣恆具有對稱性。
差分方程組的求解 隨著差分法的實際套用,產生了在計算機上求解高階稀疏矩陣問題的種種方法,其中最簡單而且常用的是點鬆弛法。對代數方程組
點鬆弛法的一般疊代格式是
是疊代序號,是任意給定的初始值,是疊代參數。當係數矩陣對稱正定時,取0<1時,稱超鬆弛。對於五點格式的差分方程組(2),存在一個最優的疊代參數>1, 與 ω =1相比, 達到同樣精度的運算量從()階降為()階,是格線點的總數。
差分方程組的求解,還有各種直接法和其他疊代法。直接法大多是高斯消去法的變形,其中心問題是如何採取適當的消去順序,使得在不影響解的精度的前提下,儘可能在運算量、存貯量及程式複雜性等方面得到好處或達到某種平衡。在疊代法方面,則還有切比雪夫疊代和共軛斜量法,它們也常作為加速手段與點鬆弛法結合使用。對於特殊形狀區域(如矩形域),則有高效的快速傅立葉變換方法和交替方向法。特別引人注目的是近年發展起來的多重格線法,其運量可達到()階。
 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法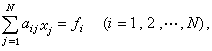 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法 偏微分方程邊值問題差分方法
偏微分方程邊值問題差分方法
