正交配置法

正交配置法（Orthogonal Collocation Method），是加權餘項法（Method of Weighted Residuals）的一種，可用於解線性以及非線性常微分方程組、偏微分方程組的初值和邊值問題。該方法特別適合求解非線性問題，與傳統差分法相比，具有計算精度高和穩定性好等優點。

基本介紹

• 中文名：正交配置法
• 外文名：Orthogonal Collocation Method
• 定義：一種加權餘項法
• 基本思想：將微分方程的未知解展開
• 套用學科：數學術語
• 範疇：數理科學

概念

正交配置法（Orthogonal Collocation Method），是加權餘項法（Method of Weighted Residuals）的一種，可用於解線性以及非線性常微分方程組、偏微分方程組的初值和邊值問題。該方法特別適合求解非線性問題，與傳統差分法相比，具有計算精度高和穩定性好等優點。

所謂加權餘項法，是將微分方程的未知解展開成一組具有可調常數的試驗函式，選擇合適的常數值，使得試驗函式充分接近於微分方程的精確解。若選用正交多項式為試驗函式，並取正交多項式的根作為配置點時，則稱為正交配置法。

基本原理

在實際套用中，求解區域常為對稱的，如為平板、圓柱、圓球，此時可構造如下的試驗函式：

該式滿足：

式中 為常數，且

滿足上式的多項式即Jacobi多項式。

正交多項式的零點，即配置點，根據Villadsen和Stewart的研究，用配置點處的解 進行計算，可以提高計算效率，簡化電腦程式，試函式的數值導數可以表示為如下：

對於圓柱對稱系統，當配置點數N=3時，上述各參數如表1所列：

表1

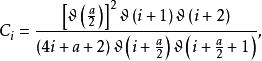
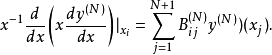
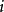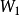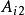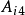1	0.29763730	0.11023111	-3.3597940	5.2924315	-3.1010284	1.1683909
2	0.63989598	0.19409673	-1.3980385	-1.5627540	4.3197367	-1.3589442
3	0.88750181	0.16442216	0.69721650	-3.6766754	-1.1267583	4.1062172
4	1	1/32	-1.2266754	5.4010626	-19*.174383	15

將上述各參數帶回待求偏微分方程(組)，原方程轉化為常微分方程組，此時即可用Runge-Kutta法求解，也可將獲得的常微分方程繼續用正交配置法離散為代數方程組。