基本介紹
- 中文名:差分格式
- 外文名:difference scheme
- 套用:數值計算
- 類型:方式方法
- 相關:離散化
差分格式簡介
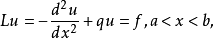



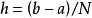






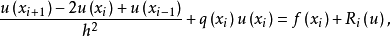



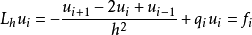









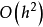


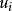


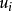



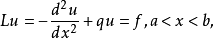



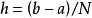






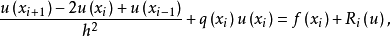



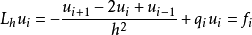









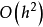


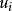


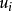


差分格式是數值計算方法中微分以及偏微分導數的一種離散化方法,即用相鄰兩個或者多個數值點的差分取代偏微分方程中導數或者偏導數的一種算法。 選擇差分格式是...
在數學中,差分法(difference methods,簡稱DM),是一種微分方程數值方法,是通過有限差分來近似導數,從而尋求微分方程的近似解。“差分法”是在比較兩個分數大小時,...
有限差分方法(finite difference method)一種求偏微分(或常微分)方程和方程組定解問題的數值解的方法,簡稱差分方法。...
介紹 兩層差分格式(two-level difference schemes )差分格式的一種.指僅涉及t=t。與t=t}+}兩個相繼時間層格點的差分格式.例如,近似一維擴散方程 是兩層...
介紹 多層差分格式(multi-level difference schemes )差分格式的一種.指聯繫多於兩個時間層上格點的解值的差分格式.例如近似一維擴散方程 是三層格式.為使用這一...
顯式差分格式屬於數值格式中的一種...... 顯式差分格式V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:3次歷史版本 最近更新: 創建者:百科ROBOT...
差分格式精確度階(order of accuracy of a finite difference scheme)偏微分方程數值解法概念之一指度量差分方程與微分方程近似程度的量.對於一個相容近似。...
介紹 差分格式相容性(consistency of a finite difference scheme)偏微分方程數值解法概念之一指微分方程與逼近它的某一個差分方程間的關係.把微分方程的光滑解代...
定義 耗散型差分格式(dissipative difference schemes)對稱雙曲型方程組的一類差分格式.設差分格式的局部放大矩陣為G(二,}t,}>,式中寧一}xk,以凡記G的特徵值...
定義 差分格式依賴區域(numerical domain of dependence of a finite difference scheme)初值線上的某一點集.用一差分格式求解偏微分方程初值問題時,在求解區域內...
顯示差分格式的缺點之一是:用來逼近離散點xi處偏導數的差分格式涉及到的格線點數,最少要比此差分格式截斷誤差的階數大1。這樣要使用較高精度的差分格式,就需要...
差分格式收斂性(convergence of a finte difference scheme)偏微分方程數值解法概念之一指差分方程解與其所近似的微分方程解之間的關係.令(二,t)是差分方程求解...
有限差分,是微分方程解的近似值。有限差分是形式為f(x+b)-f(x+a)的數學表達式。如果有限差分除以b-a,則得到差商。 有限差分導數的逼近在微分方程數值解的...
差分格式局部截斷誤差(local truncation errorof a finite difference scheme)度量微分方程的光滑解對一個差分格式近似滿足程度的量一般地,微分方程的解不精確滿足用...
中心差分格式,就是界面上的物理量採用線性插值公式來計算。在對流項中心差分的數值解不出現振盪的參數範圍內,在相同的格線節點數下,採用中心差分的計算結果要比...
差分對應離散的運算,差分計算是使用差分進行的運算。...... 差分,又名差分函式或差分運算,差分的結果反映了離散量之間的一種變化,是研究離散數學的一種工具。...
差分位置概述 由天線接收的電磁信號被送入接收機。理想的接收機抑制所有不需要的噪聲,包括其他信號,並對需要的信號不增加任何噪聲或干擾。不管信號的形式或格式如何...
高解析度格式是求解具有間斷解的微分方程中構造的一種無振盪或基本無振盪的,且對激波解具有高解析度的差分格式。自1983年Harten提出TVD格式以來,高解析度格式得到了...
差分環繞是一種新型環繞技術,其方法是通過左右聲道時間延遲較短時間來使人耳在接收音頻時更自然,更符合結構學和外界感知,其現在有兩大分類,一種是rockbox播放器...
分量模擬視頻(Y'P'BP'R)包括了多個差分格式。此類格式包括了標準清晰度(SD)、增強型清晰度(ED)以及高清晰度(HD)視頻。SD視 頻包括了基於NTSC的480i (aka ...
