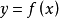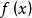中心差分

中心差分格式，就是界面上的物理量採用線性插值公式來計算。在對流項中心差分的數值解不出現振盪的參數範圍內，在相同的格線節點數下，採用中心差分的計算結果要比採用迎風差分的結果誤差更小。

基本介紹

• 中文名：中心差分
• 外文名：Central difference
• 含義：採用線性插值公式來計算
• 優點：比採用迎風差分的結果誤差更小

簡介

設函式 在等距節點 上的值 為已知，這裡 h 是常數，稱為步長(step size)。

記，稱其為在 處以 h 為步長的向前差分(forward difference)，被稱作向前差分運算元，簡稱差分運算元(difference operator)；

稱為向後差分 (backward difference)， 為向後差分運算元；

稱為中心差分(central difference，centered difference)，稱為中心差分運算元。

分類

一階差分

，，也可稱為一階有限差分，簡稱一階差分(difference of first order)。

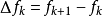
二階差分

通過一階差分可以定義二階差分。

例如 。

由於中心差分用到和不是函式表上的值，二階中心差分應寫成

高階差分

用同樣的方法可以定義高階差分(difference of higher order，higher difference)：

套用

中心差分及一階迎風格式優缺點的討論：

1、在對流項中心差分的數值解不出現振盪的參數範圍內，在相同的格線節點數下，採用中心差分的計算結果要比採用迎風差分的結果誤差更小。

2、一階迎風格式離散方程係數aE及aW永遠大於零，因而無論在任何計算條件下都不會引起解的振盪，永遠可以得出在物理上看起來是合理的解。正是由於這一點，使一階迎風格式在過去半個世紀中得到廣泛的採用。

3、由於一階迎風格式的截差階數低，除非採用相當細密的格線，其計算結果的誤差較大。近10年來，對於一階迎風等低階格式的套用，某些國際學術刊物已提出了限制條件。

4、 一階迎風格式的使用實踐也為構造性能更優良的離散格式提供了有益的啟示，應當在迎風方向上獲取比背風方向上更多的信息以較好地反映對流過程的物理本質。在最近20餘年中發展起來的對流項離散格式，如二階迎風、三階迎風及QUICK格式都吸取了這一基本思想。

5、軟體的調試過程或計算的中間過程（如多重格線的粗格線上、非線性問題的疊代過程）中，一階迎風由於其絕對穩定的特性仍有其套用的價值。