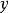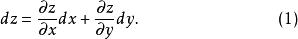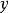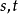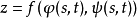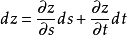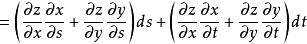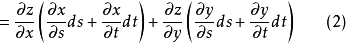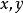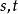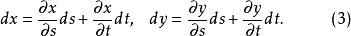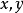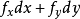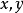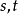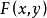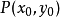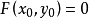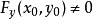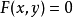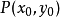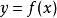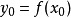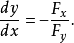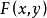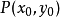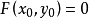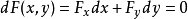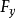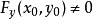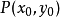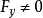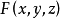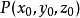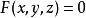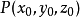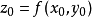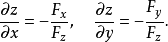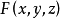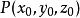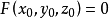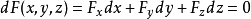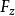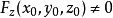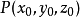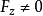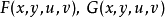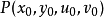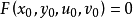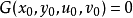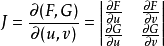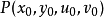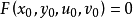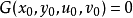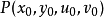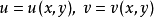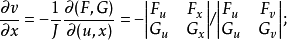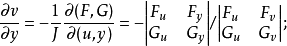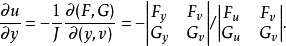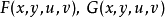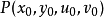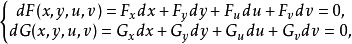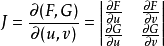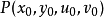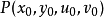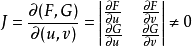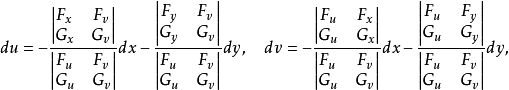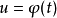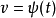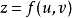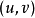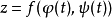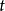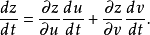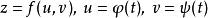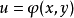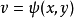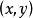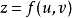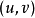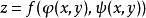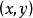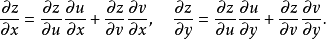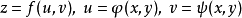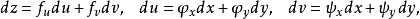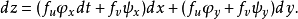一階微分形式不變性

一階微分形式不變性是指：無論u，v是自變數還是中間變數，函式z=f(u,v)的全微分形式是一樣的。此性質的好處是：一方面是可以不用區分變數直接利用一元函式的微分性質計算；另一方面是不用區分變數是自變數、因變數還是中間變數，以及它們的結構問題就可以利用微分性質直接計算。

基本介紹

• 中文名：一階微分形式不變性
• 外文名：first order differential form invariance
• 學科：數學
• 領域範圍：數學分析
• 屬性：多元函式微分學

定義

若以和為自變數的函式可微，則其全微分為

如果，作為中間變數又是自變數的可微函式

由於複合函式是可微的，其全微分為

由於又是的可微函式，因此同時有

將（3）式代入（1）式，得到與（2）式完全相同的結果。這就是關於多元函式的一階（全）微分形式不變性。
這是一階全微分的一個非常重要的性質，有了這個“形式不變性”作保證，對於一個函式就可以按照是自變數去求它的微分，而無需顧忌究竟真的是自變數，還是一個隨自變數變化的中間變數。

在微積分的教與學的過程中，利用這個性質求解較複雜的多元函式特別是複合函式，隱函式的偏導數，實用方便，簡單易行。

在隱函式求導中的套用

隱函式存在定理是微積分中的難點，一般的教材介紹這一部分時，儘管對定理的證明不做要求，但是推導偏導數的過程複雜，公式繁多，導致許多學生在求隱函式的偏導數時，常會出錯，但若利用一階微分的形式不變性對方程兩邊同時求微分，則可減少此類錯誤。

隱函式存在定理1

設函式在點的某一領域內具有連續的偏導數，且，。則方程在點的某一領域內恆能惟一確定一個單值連續且具有連續偏導數的函式，它滿足條件，並有

證明 設函式在點的某一領域內具有連續的偏導數，且，則函式可微。於是。由於連續，且，由連續函式的保號性，存在的某一領域，在該領域內，。於是可得結論成立。

隱函式存在定理2

設函式在點的某一領域內具有連續的偏導數，且，。則方程在點的某一領域內恆能惟一確定一個單值連續且具有連續偏導數的函式，它滿足條件，並有

證明 設函式在點的某一領域內具有連續的偏導數，且，則函式可微。於是。由於連續，且，由連續函式的保號性，存在的某一領域，在該領域內，。於是得，由一階全微分形式不變性，可知結論成立。

隱函式存在定理3

設函式在點的某一領域內有對各個變數的連續偏導數，且，，且偏導數所組成的函式行列式（或雅克比行列式）

在點不等於零，則方程組，在點的某一領域內能惟一確定一組單值連續且具有連續偏導數的函式，它們滿足條件，並有

證明 設函式在點的某一領域內具有連續的偏導數，則函式可微。於是

當偏導數所組成的函式行列式（或雅克比行列式）

在點不等於零時，由連續函式的保號性，存在的某一領域內，於是由Gramer法則得

由一階全微分形式不變性可得結論成立。

在複合函式求偏導中的套用

複合函式的中間變數均為一元函式的情形

設函式及都在點可導，函式在對應點具有連續偏導數，則複合函式在對應點可導，且其導數可用下列公式計算：

證明都可微，因此，由一階微分形式不變性可得

從而

所以上述結論成立。

複合函式的中間變數均為多元函式的情形

設函式及都在點可導，函式在對應點具有連續偏導數，則複合函式在對應點可導，且其導數可用下列公式計算：

證明都可微，因此，由一階微分形式不變性可得

從而

所以上述結論成立。