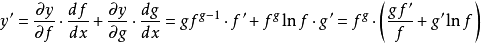基本介紹
- 中文名:冪指函式
- 外文名:power-exponential function
- 函式推廣:廣義冪指函式
- 特點:既像冪函式 又像指數函式
定義,具體例子,函式極限,一般方法,待定型,肯定型,典例分析,求導方法,
定義
冪指函式指數和底數都是變數的函式,形如 是數集)的函式稱為冪指函式,其中 u,v 是 E 上的函式。
是數集)的函式稱為冪指函式,其中 u,v 是 E 上的函式。

當不給出 u(x)與 v(x) 的具體形式時,總要求 。因此,冪指函式可改寫成由
。因此,冪指函式可改寫成由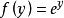 與
與 複合而成的函式 f(g(x)),從而當 u,v 連續時它連續,u,v 可微時它也可微。
複合而成的函式 f(g(x)),從而當 u,v 連續時它連續,u,v 可微時它也可微。

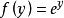

冪指函式既像冪函式,又像指數函式,二者的特點兼而有之。作為冪函式,其冪指數確定不變,而冪底數為自變數;相反地,指數函式卻是底數確定不變,而指數為自變數。冪指函式就是冪底數和冪指數同時都為自變數的函式。這種函式的推廣,就是廣義冪指函式。
具體例子
在x>0時,函式曲線是連續的,並且在x=1/e處取得最小值,約為0.6922,在區間(0,1/e]上單調遞減,而在區間[1/e,+∞)上單調遞增,並過(1,1)點。 圖1.最簡單的冪指函式
圖1.最簡單的冪指函式
 圖1.最簡單的冪指函式
圖1.最簡單的冪指函式函式極限
本段中所有 的記號,表示的是各種可能的趨向,即 *可以是a、a-0、a+0 、∞ 、-∞ 或+∞ 。
的記號,表示的是各種可能的趨向,即 *可以是a、a-0、a+0 、∞ 、-∞ 或+∞ 。

一般方法
利用恆等變形(即換底變形)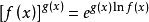 及複合函式
及複合函式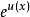 求極限法則
求極限法則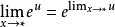 ,有
,有
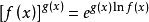
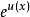
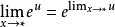

待定型





所以冪指函式極限 僅有三種待定型:
僅有三種待定型: 型、
型、 型、
型、 型。
型。




肯定型
冪指函式的極限 除了上述三種待定型外沒有第四種待定型了。
除了上述三種待定型外沒有第四種待定型了。

若 、
、 ,因為規定l了
,因為規定l了 ,所以必有
,所以必有 ,則
,則




(1) ,(i)
,(i) ,
,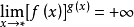 ;(ii)
;(ii) ,
, ;
;


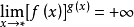


(2) ,
, ,
, ;
;



(3) ,(i)
,(i)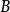 為
為 ,
, ;(ii)
;(ii)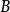 為為
為為 ,
,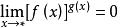 ;
;

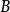


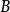

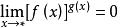
(4)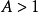 ,(i)
,(i)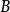 為
為 ,
, ;(ii)
;(ii)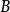 為為
為為 ,
, ;
;
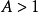
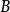


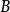


(5) 為+
為+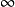 ,(i)
,(i) 或
或 ,
,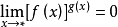 ;(ii)
;(ii) 或
或 ,
, 。
。

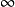


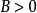


典例分析
(1)求 ,
,

解 這個極限式“ 型”待定型,先求
型”待定型,先求 ,所以
,所以




解這個極限式是“ 型”待定型,先求
型”待定型,先求 ,其中
,其中





(3)求



所以 。
。

注 本題也可以等價無窮大替代,或經過放大縮小 後再用夾逼準則計算。
後再用夾逼準則計算。

(4)求 。
。

解這個極限式是“ 型”待定型,先計算
型”待定型,先計算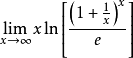 ,由於
,由於 ,可知
,可知 是
是 時的無窮小量,利用等價無窮小關係
時的無窮小量,利用等價無窮小關係 ,可得
,可得

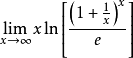





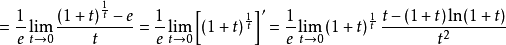


注 (1)這裡“ 型”待定型中不能先把“底的極限1”先算出來,錯成
型”待定型中不能先把“底的極限1”先算出來,錯成 。
。


(2)解這種問題時除了使用洛必達法則外,經常會用到等價無窮小替代及換元方法。
求導方法
下面給出一般冪指函式的求導方法。為書寫方便,把f(x)和g(x)分別用f和g代替,即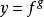
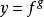
指數求導法
由於冪指函式定義中f(x)>0,因此可以利用對數的性質將函式改寫。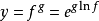 ,再對指數函式進行求導。
,再對指數函式進行求導。
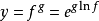
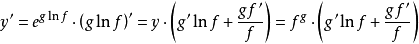
對數求導法
這種方法是在兩邊取對數,再利用隱函式的求導法則求出y‘。



多元複合函式求導法
根據一元與多元函式複合的求導法則, 的導數為
的導數為