發散級數

發散級數指不收斂的級數。一個數項級數如果不收斂，就稱為發散，此級數稱為發散級數。一個函式項級數如果在（各項的定義域內）某點不收斂，就稱在此點發散，此點稱為該級數的發散點。按照通常級數收斂與發散的定義，發散級數是沒有意義的。然而為了實際的需要，可以確立一些法則，對某些發散級數求它們的“和”，或者說某個發散級數在特定的極限過程中，逐漸逼近某個數。但是在實際的數學研究以及物理等其它學科的套用中，常常需要對發散級數進行運算，於是數學家們就給發散級數定義了各種不同的“和”，比如Cesàro和，Abel和，Euler和等，使得對收斂級數求得的這些和仍然不變，而對某些發散級數，這種和仍然存在。

基本介紹

• 中文名：發散級數
• 外文名：divergent series
• 指：不收斂的級數
• 比如：級數1+2+3+4……和1-1+1-1……
• 遵照：柯西意義

簡介

發散級數指不收斂的級數。一個數項級數如果不收斂，就稱為發散，此級數稱為發散級數。一個函式項級數如果在（各項的定義域內）某點不收斂，就稱在此點發散，此點稱為該級數的發散點。

記無窮級數.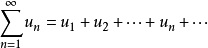

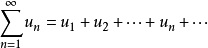
當n→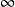時，若部分和數列{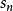}有極限s，即則稱無窮級數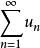收斂，且稱s為無窮級數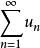的和，並記為

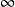
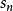
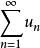
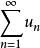
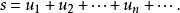
若數列{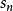}極限不存在，則稱無窮級數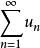發散。

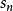
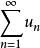
總之，發散是收斂的否定。

級數的求和

(summ ation ofseries)

賦予某些發散級數以“和”的法則，按照柯西的定義，收斂級數以其部分和的極限為和，這種和是有限（項的）和的直接推廣，可稱為柯西和，按照這種定義，發散級數是沒有和的，從而只是沒有實際意義的數學記號而已。然而數學的發展表明，完全排斥發散級數是不恰當的。例如，函式 1/(1+x²) 在 x=±1 時是有意義的，而在其泰勒展開式中令x=±1卻得到發散級數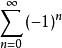，這說明它應該是有“和”的。

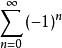
再如連續函式的傅立葉級數可能是發散的，但其前 n 個部分和的算術平均當 n→∞ 時卻總有確定極限，這說明這些級數是可以有“和”的。在這些情況下，人們需要也可以對某些發散級數的“和"作出合理的解釋。於是出現這樣一些法則，用它可以確定任意級數有和或者沒有和，並在前一種情況下，給出求和的方法，這種法則就稱為級數的求和。

這種法則是很多的，如果將某個這種法則稱為 M 求和法，而按 M 求和法是有和的，並可求出和為S，則稱為 M 可和的，並記為。

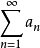
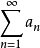
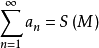
級數求和主要是針對發散級數提出來的。每一種求和法都能使某些發散級數有和，同時又希望按照它，所有的收斂級數都是可和的，並且所求出的和與其柯西和相等，這樣的級數求和方法就稱為正則的。級數的正則求和法是收斂性（柯西和）概念的直接推廣，在調和分析、通近論等數學學科中有很多套用。

每一種有意義的級數求和法表面上都有很重的主觀定義色彩，但在數學內部多半都可找到它的深刻背景，像阿貝爾求和法，源於關於泰勒級數的阿貝爾極限定理；而算術平均求和法，就與傅立葉級數部分和的性態有關。