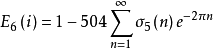朗伯級數是一種特殊形式的級數,也譯作蘭伯特級數等,形如∑∞n-1(anxn/(1-xn))的函式項級數,其中an,x為實數,若∑an收斂,則當x≠±1時,該級數收斂;若∑an發散,則該級數的收斂域與冪級數∑anxn相同,當|x|<1時,朗伯級數的和函式φ可表示成冪級數φ(x)=∑∞n-1cnxn,其中cn=∑k|nak,即cn是下標為n的因數的那些k對應的ak之和,朗伯級數是朗伯(J.H.Lambert)首先研究的,它在某些數論問題中有用並被推廣為復級數。
基本介紹
- 中文名:朗伯級數
- 外文名:Lambert series
- 所屬學科:高等數學
- 簡介:一種特殊形式的級數
- 發現者:朗伯(J.H.Lambert)
基本介紹,相關介紹,
基本介紹
定義1 定義級數
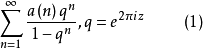
一方面,將(1)展成Fourier級數
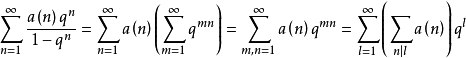
艾森斯坦(Eisenstein)級數Ek(z)的Fourier展開式為

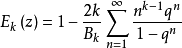
對於歐拉函式 以及麥比烏斯函式
以及麥比烏斯函式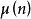 ,對應有
,對應有

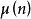
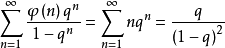
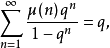
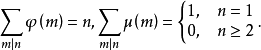
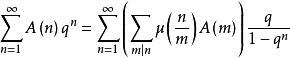
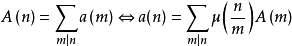
相關介紹
研究朗伯級數是為了給自守形式的表示提供方便,拉馬努金計算了許多朗伯級數的值,其中較為著名的有如下幾個,稱為拉馬努金等式。
拉馬努金等式
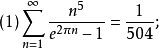

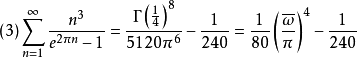
由E6(z)的變換公式有