基本介紹
- 中文名:厄米算符
- 外文名:self-adjoint operator
- 概念:表達自伴運算元的是埃爾米特矩陣
- 關鍵字:算符;厄米性;物理量;波函式
- 分類:物理學
- 特點:必為實數
簡介
物理學
基本內容
定義及性質


量子力學中力學量用厄米算符來描述

厄米算符與經典的對應

算符的厄米性對波函式的限制
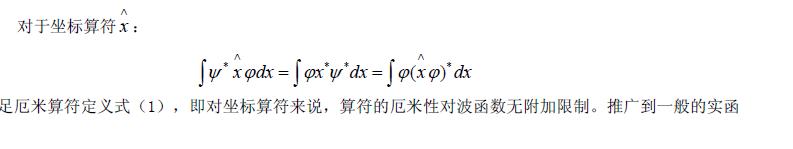





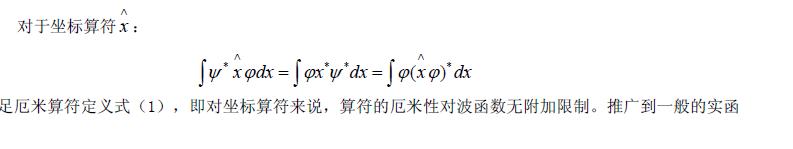
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。即厄米算符表達了一...
厄米共軛算符編輯 鎖定 在數學裡,作用於一個有限維的內積空間,自共軛矩陣。矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等;等價地說,...
一個算符若滿足乘法分配律,則稱為線性算符。如▽(ψ2+ψ1)=▽ψ2+▽ψ1若滿足∫ψ1*Rψ2dτ=∫ψ2(Rψ1)*dτ 則稱為自共軛算符。量子力學需要用...
若A=A*,A是它本身的伴隨運算元,則A稱為自伴隨運算元,在實內積空間中,自伴隨運算元稱為對稱運算元,在復內積空間中稱為厄米運算元.在量子力學中,相應物理上可觀測量的...
厄密算符的平均值定理I:體系任何狀態ψ下,其厄密算符的本徵值必為實數。...... 厄密算符的平均值 定理I:體系任何狀態ψ下,其厄密算符的本徵值必為實數。...
一個算符的復共軛算符,是將該算符中的復量替換成該復量的共軛復量。...... 厄米算符 算符的復共軛算符,是由該算符中的復量換成共軛復量構成。在量子力學...
使問題從一種狀態變化為另一種狀態的手段稱為操作符或算符。算符在單獨存在時是沒有什麼意義。操作符可為走步、過程、規則、數學運算元、運算符號或邏輯符號等。...
厄密是量子力學領域的一個專有辭彙。如果說兩個物理量是對易的,說明兩個物理量能同時被測定。所有可觀察的物理量都相應厄密算符。...
量子力學中,哈密頓算符(Hamiltonian) H為一個可觀測量(observable),對應於系統的的總能量。一如其他所有算符,哈密頓算符的譜為測量系統總能時所有可能結果的集合...
動量算符是在量子力學中表示微觀粒子的動量的算符。動量算符是表示力學量的厄米算符。...
麥可·貝里與喬·基廷(Jon Keating)推測 H實際是經典哈密頓量xp的某種量子化,與 xp相應的最簡單的厄米算符為這一對希爾伯特-波利亞猜想的改進被稱為貝里猜想...
量子力學中,可觀測量在數學上常以厄米算符(Hermitian)或自伴算符來表示。此算符的本徵值集合代表測量可能結果的集合。對於每個本徵值而言,存在有一個對應的本徵...
波函式態矢量在特定基底中的分量,可用列矩陣或用函式表示; 任意算符的本徵函式系表象的基;不同表象不同基,不同坐標系;本徵函式基矢;厄米算符的本徵函式系一...
§3.5 厄米算符本徵函式的正交性§3.6 算符與力學量的關係§3.7 算符的對易關係兩力學量同時有確定值的條件不確定關係§3.8 力學量期望值隨時間的變化守恆...
量子力學五大假設是指微觀體系的運動狀態由相應的歸一化波函式描述;微觀體系的運動狀態波函式隨時間變化的規律遵從薛丁格方程;力學量由相應的線性厄米算符表示;力學量...
3.2 厄米算符的本徵值與本徵函式 3.3 共同本徵函式 3.3.1 不確定度關係的嚴格證明 3.3.2 (l2,lz)的共同本徵態,球諧函式 3.4 連續譜本徵函式的“...
§2 算符§2-1 定義§2-2 算符的代數運算§2-3 作用於左矢的算符§2-4 厄米算符和么正算符§2-5 投影算符§3 本徵矢量和本徵值§3-1 定義...
第4章量子力學中的力學量4.1力學量和線性厄米算符4.2力學量取確定值的態4.2.1坐標算符4.2.2動量算符4.2.3角動量算符4.3展開假定測量和連續譜4.3.1展開假定...
粒子數表象是以粒子數算符的一組完備本徵矢,來描述量子力學學規律的表示方法。在粒子數表象中,所有可觀測量對應的厄米算符,都可以用粒子數升降算符來進行表示。...
設有一組彼此對易,且函式獨立的厄米算符A(A1,A2,……),它們的共同本徵函式記為ψk,k是一組量子數的籠統記號。設給定k之後就能夠確定體系的一個可能狀態,則...
有正交性並已歸一化的函式叫做“正交歸一化函式”。在量子力學中總是選取正交歸一化函式作為力學量的本徵函式。量子力學中有意義的物理量都用一個線性厄米算符來...
§2.3 物理可觀測量對應於厄米算符§2.4 坐標、動量算符,基本對易關係§2.5 坐標表象中動量算符的表示§2.6 其他物理可觀測量的量子力學算符習題...
