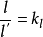無量綱化（nondimensionalize 或者dimensionless）是指通過一個合適的變數替代，將一個涉及物理量的方程的部分或全部的單位移除，以求簡化實驗或者計算的目的，是科學研究中一種重要的處理思想。
所謂合適的變數，往往利用相似準則求得，例如牛頓數，它是作用力與慣性力的比值，是一個無量綱數。兩個流動的動力相似，模型與原型牛頓數Ne應相等，這是流動重要的相似準則，也稱為牛頓相似準則。
無量鋼化的處理思想已經擴展到物理量之外。
基本介紹
- 中文名：無量綱化
- 外文名：nondimensionalize
處理方法（物理相似）,實驗模型設計,如何選擇相似準則,常用相似準則適用範圍,套用示例,格子玻爾茲曼方法中的無量綱化,二維湍流及水波數值模,
試驗中經常遇到的問題：
一、變數多
實驗中應測哪些量，是否所有的物理量都測。
實驗數據如何整理，用什麼樣函式關係來表示實驗研究的物理過程。如：影響管內強迫對流換熱的物理量有6個， 對流傳熱係數h=f(u,d,λ,ρ,c,p,μ)。
二、試驗由於種種原因（場地、經費等）無法復現原模型，如何進行試驗？
無法在實物進行實驗時，如何建立實驗模型。
模型上獲得的試驗關聯式能否套用到實物中，如何用到實物上去。
如何利用有限的資源，減少實驗次數/計算時間，同時又能獲得具有通用性的規律？
處理方法（物理相似）
相似首先出現在幾何里，如兩個三角形相似時，則他們的對應邊成比例，對應角相等。
物理相似：對於同類的物理現象，在相應的時刻、相應的位置、與現象有關的物理量一一對應成比例。
（一）只有同類問題才能談相似：同類物理現象是指能夠用相同形式和相同內容的微分方程式所描寫的現象。反之如電場與溫度場之間形式相仿，但內容不同，不是同類現象，只能做類比。（二）與現象有關的物理量一一對應成比例：要求每個物理量都要各自相似。例如，對流傳熱除了時間空間外還涉及到速度，溫度，熱物性等參數。 （三）非穩態問題：要求相應的時刻各物理量的空間分布相似。
回到之前的問題，為從模型流動上預測出原型流動的結果，就必須使兩者在流動上相似，即兩個互為相似流動的對應部位上對應物理量都有一定的比例關係。
流動相似：表征流動過程的物理量按其性質主要有三類，即表征流場幾何形狀的，表征流體微團運動狀態的和表征微團動力性質的，因此，流動的相似主要包括流場的幾何相似、運動相似和動力相似。
流場在滿足以上關係時，我們就稱為兩個流場力學相似。
相似 → 物理相似 → 流動相似（幾何相似：如長度、面積、體積，運動相似：如速度、加速度、流量，動力相似：如質量力、表面力、動量）
幾何相似
保持幾何相似是模型實驗最基本的要求。幾何相似是指模型與原型的全部對應線性長度的比例相等，即
式中kl為長度比尺或比例。
只要模型與原型的全部對應線性長度的比例相等，則它們的夾角必相等。由於幾何相似，模型與原型的對應面積、對應體積也分別互成一定比例，即：
模型與原型各相應長度保持保持比例不變，兩流動幾何相似。
運動相似
運動相似是指模型與原型的流場所有對應點、對應時刻的流速方向相同而大小成比例。
動力相似
動力相似是指模型與原型的流場所有對應點作用在流體微團上的各種力彼此方向相同，而它們大小的比例相等。
以上三種相似是互相聯繫的：
流場的幾何相似是流動力學相似的前提條件；
動力相似是決定運動相似的主導因素；
而運動相似則是幾何相似和動力相似的表現。
因此，模型與原型流場的幾何相似、運動相似和動力相似是兩個流場完全相似的重要特徵。
有了以上關於幾何學量、運動學量和動力學量的三組比尺，模型與原型流場之間各物理量的相似比尺就可以相互換算。
由於兩個流場的密度比尺常常是已知的或者是已經選定的，故做流體力學的模型實驗時，經常選取選取密度ρ，長度l和速度v作為獨立的基本變數，即利用k_ρ，k_l和k_v推導其他基本比尺。
實驗模型設計
如何選擇相似準則
確定長度比尺k_l：根據實驗條件或模擬計算條件等； Ø選擇流體介質：一般採用同一介質k_ρ=1； Ø選擇相似準則：在幾何相似的前提下，選擇合適的動力相似準則。
相似準則數越多，模型實驗的設計越困難，甚至根本無法進行。
近似的模型實驗方法，即在設計模型和組織模型實驗時，在與流動有關的相似準則中考慮那些對流動過程起主導作用的相似準則（決定性準則），而忽略那些對流動過程影響較小的相似準則（非決定性準則），達到模型與原型流動的近似相似。
常用相似準則適用範圍
在模擬流體實驗時，最經常用到的三個準則數為雷諾數Re ，弗勞德數Fr 和歐拉數Eu 。
雷諾數Re：主要受水流阻力即粘滯力作用的流體流動，凡是有壓流動，重力不影響流速分布主要受粘滯力的作用，這類液流相似要求雷諾數相似。另外，處於水下較深的運動潛體，在不至於使水面產生波浪的情況下，也是以雷諾數相等保證液流動力相似。如層流狀態下的管道、隧洞中的有壓流動和潛體繞流問題等。
弗勞德數Fr：凡有自由水面並且允許水面上下自由變動的各種流動( 重力起主要作用的流動) ,如堰壩溢流、孔口出流、明槽流動、紊流阻力平方區的有壓管流與隧洞流動等。
歐拉數Eu： 兩液流的雷諾數相等，歐拉數也相等；兩液流的弗勞德數相等，歐拉數也相等。出現負壓或存在氣蝕情況的液體，需考慮歐拉數相等來保證液流相似。
套用示例
格子玻爾茲曼方法中的無量綱化
以一個二維平直通道內流動為例，若模擬中取格子單位下的參數為δx=δy=1，δt=1，c_s=1/√3，ν′=0.1，L′=Nx∗δx=1000，此處Nx代表格線數。
考慮實際空氣聲速c=332m/s，運動粘度係數ν=1.5∗〖10〗^(-5)，得：
ku=c/c_s=576m/s，k_l=k_ν/k_u=2.6∗〖10〗^(-7)，則L=2.6∗〖10〗^(-4)。
理解為將"L=2.6∗10-4"實際大小利用相似準則，長度比尺為k_l=2.6∗〖10〗^(-7)，將實際大小擴大為了1000*1000的模型。
二維湍流及水波數值模
選取實際流場特徵長度為l、特徵速度為U、聲速為C、時間為T、壓力為P、密度為ρ、體積力為F、運動粘性係數為ν。格子法計算流場時特徵長度取l’，這樣相似比
k_l=l/l^′ , k_u=c/c_s
其他參數可按上述相似率確定：
u^′=u/k_u , ν′=ν/k_ν =ν/(k_l k_u )
T′=T/k_T =T/(k_l/k_u ) , ρ′=ρ/k_ρ =ρ/(k_l k_u )
"P"′=P/k_P "=" P/(k_l k_u ) F′=F/k_g =G/(k_l k_u 2)
這樣，就可以實現格子Boltzmann流體和實際流體之間物理參數的相互轉換。
