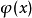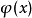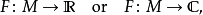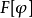基本介紹
- 中文名:泛函導數
- 外文名:functional derivative
定義,泛函導數,泛函微分,正式表述,性質,確定的泛函導數,公式,例子,δ函式作為測量函式,
定義
在變分法中,泛函通常表示成函式、函式導數以及自變數的積分。例如考慮泛函
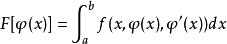
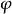
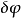
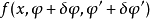
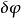
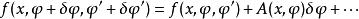
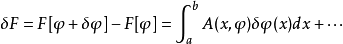
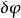
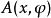
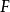
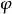

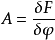
泛函導數
對任何測量函式

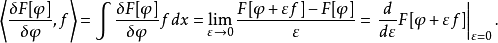
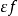
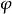
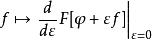
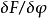
把函式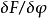 看作
看作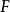 在
在 處的梯度,
處的梯度,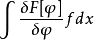 看作在
看作在 處沿方向
處沿方向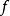 的方嚮導數,則類似於向量微積分,梯度與某個方向向量的內積就給出了這個方向的方嚮導數。
的方嚮導數,則類似於向量微積分,梯度與某個方向向量的內積就給出了這個方向的方嚮導數。
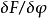
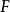

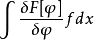

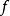
泛函微分
泛函 的微分就是
的微分就是

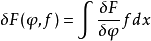
用一個啟發性的觀點來看,
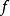
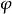
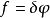
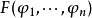
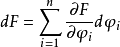
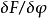
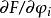

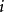
正式表述
通過更具體地定義函式空間,泛函導數的定義可以在數學上更準確、正式。例如,當函式空間是巴拿赫空間時, 泛函導數就是著名的弗雷歇導數, 而在更一般的局部凸空間上就是加托導數。注意,希爾伯特空間是巴拿赫空間的特例。更正式的處理使我們能夠將普通微積分和數學分析中的許多定理推廣為泛函分析中對應的定理,此外還能得到大量的新定理。
性質
與函式的導數類似,泛函導數滿足下列的性質(其中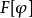 和
和 都是泛函):
都是泛函):
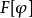

- 線性:
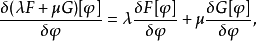

- 積法則:
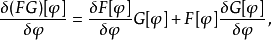
- 鏈式法則:
若F和G為兩個泛函,則

若當中的G為一個普通的可導函式g,則上式化為
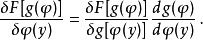
確定的泛函導數
有一類常見的泛函,能表示成一個函式及其導數的積分的形式。對於這類泛函,可以給出一個計算泛函導數的公式。
公式
對於泛函
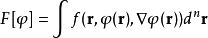
以及在積分區域的邊界上取0的函式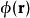 ,由之前的定義
,由之前的定義
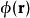
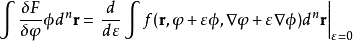
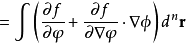
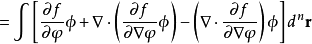
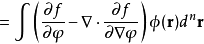
因為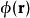 是任意的函式,由變分法基本引理,得泛函導數為
是任意的函式,由變分法基本引理,得泛函導數為
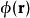
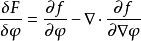
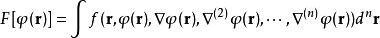

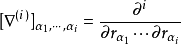
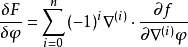
例子
托馬斯-費米動能泛函
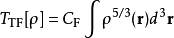 被積函式不含
被積函式不含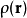 的導數,所以泛函導數
的導數,所以泛函導數
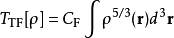
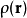
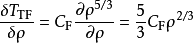
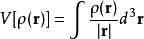

魏茨澤克動能泛函
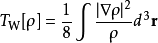
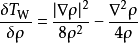
熵
連續隨機變數的熵是其機率密度函式的泛函


指數
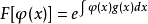
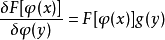
函式的泛函導數
函式可以像泛函那樣寫成一個積分的形式
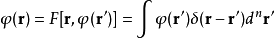
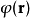
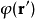

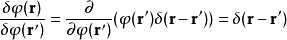
疊代函式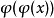 的泛函導數
的泛函導數
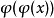
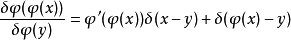
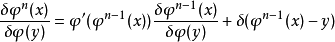

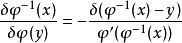
δ函式作為測量函式
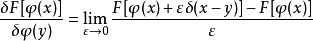
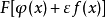

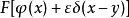
上面給出的定義是基於一種對所有測量函式f都成立的關係,因此有人可能會想,它在f是一個指定的函式(比如說狄拉克δ函式)時也應該成立。但是,δ函式不是一個合理的測量函式(甚至都不是一個真正的函式)。
在定義中,泛函導數描述了整個函式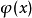 發生微小變化時,泛函
發生微小變化時,泛函 如何變化。其中,
如何變化。其中,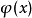 的變化量的具體形式沒有指明,但應該在整個定義區間上都有變化。使用δ函式形式的擾動表明函式只在點
的變化量的具體形式沒有指明,但應該在整個定義區間上都有變化。使用δ函式形式的擾動表明函式只在點 處變化,其他的點都沒有變化。
處變化,其他的點都沒有變化。