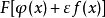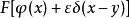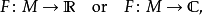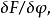光滑泛函

在數學和理論物理中，泛函導數是方嚮導數的推廣。後者對一個有限維向量求微分，而前者則對一個連續函式（可視為無窮維向量）求微分。它們都可以認為是簡單的一元微積分中導數的擴展。數學裡專門研究泛函導數的分支是泛函分析。

基本介紹

• 中文名：光滑泛函
• 外文名：Functional derivative
• 領域：數學

簡介

在數學和理論物理中，泛函導數是方嚮導數的推廣。後者對一個有限維向量求微分，而前者則對一個連續函式（可視為無窮維向量）求微分。它們都可以認為是簡單的一元微積分中導數的擴展。數學裡專門研究泛函導數的分支是泛函分析。

定義

設有流形M代表（連續/光滑/有某些邊界條件等的）函式 φ 以及泛函F：

則F的泛函導數，記為是一個滿足以下條件的分布：

對任何測量函式f：

用的一次變分代替就得到F的一次變分；

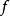
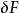
在物理學中，通常用狄拉克δ函式{\displaystyle \delta (x-y)}，而不是一般的測試函式{\displaystyle f(x)}, 來求出點{\displaystyle y}處的泛函導數(這是整個泛函變分的關鍵點，就像偏導數是梯度的一個分量):

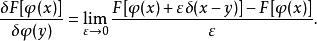
這適用於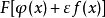可以展開成的級數時 (或者至少能展為1階). 但是這一表達在數學上並不嚴格，因為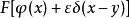一般而言並未定義。

正式表述

通過更仔細地定義函式空間，泛函導數的定義可以更準確、正式。例如，當函式空間是一個巴拿赫空間時, 泛函導數就是著名的Fréchet導數, 而這在更一般的局部凸空間上使用加托導數。注意，著名的希爾伯特空間是巴拿赫空間的特例。更正式的處理允許將普通微積分和數學分析的定理推廣為泛函分析中對應的定理，以及大量的新定理。