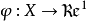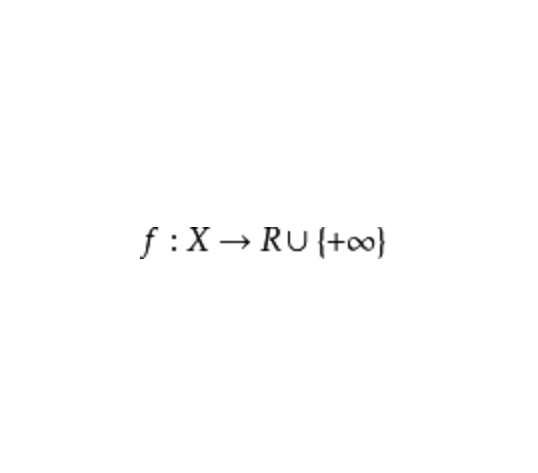基本介紹
- 中文名:弱下半連續泛函
- 外文名:weakly lower semicontinuous functional
- 定義:弱拓撲的意義下為下半連續的泛函
- 相關:泛函
- 一級學科:數學
- 二級學科:非線性分析拓撲與變分方法
簡介,泛函,弱下半連續泛函的極值,
簡介
弱下半連續泛函是指在巴拿赫空間中弱拓撲的意義下為下半連續的泛函。設 X 是巴拿赫空間,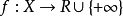 。若在 X 中取弱拓撲時 f 為下半連續(或依序列下半連續),則稱 f 為弱下半連續(相應地,依序列弱下半連續)。在臨界點理論中常用到下述結果:設 X 是自反巴拿赫空間,M 是 X 中的非空弱閉集,
。若在 X 中取弱拓撲時 f 為下半連續(或依序列下半連續),則稱 f 為弱下半連續(相應地,依序列弱下半連續)。在臨界點理論中常用到下述結果:設 X 是自反巴拿赫空間,M 是 X 中的非空弱閉集,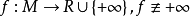 。若 f 是依序列弱下半連續的,且 f 是強制的(即,當
。若 f 是依序列弱下半連續的,且 f 是強制的(即,當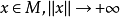 時有
時有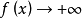 ),則 f 在 M 上可達到下確界。巴拿赫空間中的下半連續凸泛函是弱下半連續的。具有全連續梯度映射的泛函是依序列弱連續的。
),則 f 在 M 上可達到下確界。巴拿赫空間中的下半連續凸泛函是弱下半連續的。具有全連續梯度映射的泛函是依序列弱連續的。
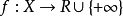
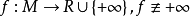
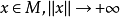
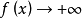
泛函
設 {y}是給定的函式集,如果對於這個函式集中任一函式y(x) 恆有某個確定的數與之對應,記為П(y(x)),則П(y(x))是定義於集合{y(x)}上的一個泛函。
泛函定義域內的函式為可取函式或容許函式, y(x) 稱為泛函П的變數函式。
泛函П(y(x))與可取函式y(x)有明確的對應關係。泛函的值是由一條可取曲線的整體性質決定的。
泛函也是一種“函式”,它的獨立變數一般不是通常函式的“自變數”,而是通常函式本身。泛函是函式的函式。由於函式的值是由自變數的選取而確定的,而泛函的值是由自變數函式確定的,故也可以將其理解為函式的函式
泛函的自變數是函式,泛函的自變數稱為宗量。
簡言之,泛函就是函式的函式。
弱下半連續泛函的極值
定義1,泛函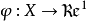 在
在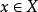 稱為弱下半連續的,是指
稱為弱下半連續的,是指 時,必有
時,必有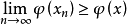 。如果以
。如果以 代替
代替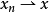 ,則稱
,則稱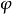 是下半連續的。
是下半連續的。
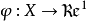
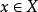

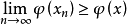

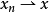
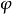
定理1,設M是X中弱閉且弱列緊的幾何,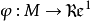 為弱下半連續泛函,則存在
為弱下半連續泛函,則存在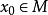 使得
使得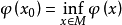 。
。
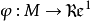
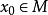
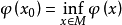
推論,設 X 是自反的巴拿赫空間,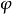 是 X 上的弱下半連續泛函。
是 X 上的弱下半連續泛函。
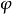
(1)如果M是X的有界弱閉子集,則必存在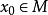 使得
使得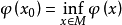 。
。
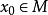
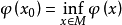
(2)如果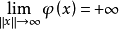 ,則必存在
,則必存在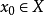 使得
使得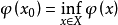 。
。
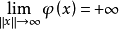
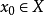
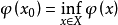
定理2,設 X 為賦范線性空間,泛函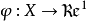 是Frèchet可微的,F(x)=gradφ(x)是緊映射,則φ弱連續。
是Frèchet可微的,F(x)=gradφ(x)是緊映射,則φ弱連續。