基本介紹
- 中文名:極小化序列
- 外文名:minimizing sequences
- 所屬學科:數學
- 所屬領域:偏微分方程
- 相關概念:希爾伯特空間、泛函等
定義,相關概念與命題,
定義
變分學和最最佳化的中心問題是求定義在Banach空間某一子集D上的泛函的最小值點。下面介紹最小值點的逼近——極小化序列。
定義1 設E是實Banach空間, ,
, 是定義在D上的實泛函。若存在
是定義在D上的實泛函。若存在 ,使得
,使得



相關概念與命題

證明: 若在D中存在 ,使得
,使得


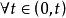


定理1 設E是實自反Banach空間,實泛函 是G-可微、強制和嚴格凸的,則
是G-可微、強制和嚴格凸的,則 的任一極小化序列弱收斂於
的任一極小化序列弱收斂於 的唯一最小值點,此時最小值點當然也是臨界點。
的唯一最小值點,此時最小值點當然也是臨界點。



證明:首先由假設知, 在整個空間E中有唯一的最小值點
在整個空間E中有唯一的最小值點 ,且為
,且為 的臨界點。
的臨界點。



再證每一個極小化序列 都是有界的:若不然,設
都是有界的:若不然,設 無界,於是存在子列
無界,於是存在子列 。由
。由 的強制性,存在
的強制性,存在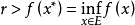 及
及 使得當
使得當 時,恆有
時,恆有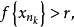 因此有
因此有




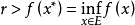


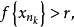


然後,由 有界,結合E自反知,存在
有界,結合E自反知,存在 及
及 ,使得
,使得 再考慮到
再考慮到 是
是 的最小值點及
的最小值點及 的弱下半連續性得
的弱下半連續性得










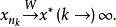
最後證 若不然,不妨設有子列
若不然,不妨設有子列 則有
則有