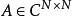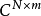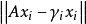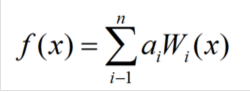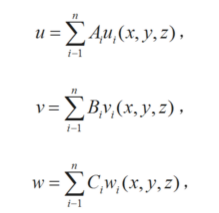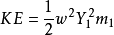瑞利一里茨法(Rayleigh-Ritz method)求泛函極小問題的極小化序列的一種直接方法。英國的瑞利於1877年在《聲學理論》一書中首先採用，後由瑞士的W.里茲於1908年作為一個有效方法提出。這一方法在許多力學、物理學、量子化學問題中得到套用。同時它也是廣泛套用於套用數學和機械工程領域的經典數值方法，它可以用來計算結構的低階自然頻率。它是直接變分法的一種，以最小勢能原理為理論基礎。通過選擇一個試函式來逼近問題的精確解，將試函式代入某個科學問題的泛函中，然後對泛函求駐值，以確定試函式中的待定參數，從而獲得問題的近似解。
基本介紹
- 中文名：瑞利一里茨法
- 外文名：Rayleigh-Ritz method
- 領域：數理科學
- 別稱：里茲法
- 提出者：里茲
- 套用：求泛函極小問題的極小化序列
簡介,方法說明,原理：,套用：,
簡介
瑞利一里茨法是通過泛函駐值條件求未知函式的一種近似方法。英國的瑞利於1877年在《聲學理論》一書中首先採用，後由瑞士的W.里茲於1908年作為一個有效方法提出。這一方法在許多力學、物理學、量子化學問題中得到套用。同時它也是廣泛套用於套用數學和機械工程領域的經典數值方法，它可以用來計算結構的低階自然頻率。它是直接變分法的一種，以最小勢能原理為理論基礎。通過選擇一個試函式來逼近問題的精確解，將試函式代入某個科學問題的泛函中，然後對泛函求駐值，以確定試函式中的待定參數，從而獲得問題的近似解。
方法說明
瑞利一里茨法允許計算瑞茨對（λi，xi），其近似特徵值問題的解
Ax=λx
其中
。
過程如下：
1.在
中計算一個正交基數 V，逼近與m個特徵向量對應的本徵空間
2.計算R<—-V*AV
3.計算R求解的特徵值
4.形成瑞茨對
人們總是可以通過
計算得到正確解。
如果使用Krylov子空間，而A是一般矩陣，那么這就是Arnoldi算法。
設l ( u)是定義在某個空間H上的泛函，考慮泛函極小問題:J(u)=min。假定
函式序列ul,uz,…稱為泛函極小問題的極小化序列。里茨法如下設w1,wz ,…構成空間H的一組完備基，因此極小化序列中每個u。均可表示為
現舉一簡單例子來說明里茨法以及它與當代有限元法的關係.仍考慮有限元法中的問題(1)(參見“有限元法”，可以證明它與下述問題等價，即求uEI; (,fl )，使得
即為。的近似解。因此問題歸結為如何確定H：(,(Z)中的完備基.當區域口是典型區域(如正方形)，則可選取代數或三角多項式之類的解析函式，作為空間H; (,fl)的完備基，這就是經典的里茨法.但當區域月為一般區域時，要尋找解析函式作為基函式，就極其困難，或根本不可能.此時有限元法卻可行.首先構造空間Ho (,(l)的有限元子空間Vh，則}1 } }2 }…，吼(對線性有限元空間，即為屋頂函式，參見“有限元法”)，組成V、的一組基函式，n=diamVh.這樣以}P}代替w，即為有限元法.
瑞利一里茨法是由瑞士物理學家、數學家裡茨(Ritz, W.)於1911年提出來的，在此之前，瑞利( Rayleigh , L,.)曾成功地運用過類似的概念，故稱瑞利一里茨法.
原理：
此法假定待求函式f(x)為n個已知函式 Wi(x)的線性組合：
式中αi為未知常係數。通過由f(x)組成的泛函式[f(x)]取駐值的條件(駐值條件對應於已知的物理定律或定理)得到n個方程，
由此解出n個未知常係數αi，從而得到f(x)。這一理論還可推廣到多維問題。
在求解彈性體位移時，先假定彈性體內沿x、y、z方向的位移u、v、w分別由一系列已知的滿足彈性體全部位移邊界條件的連續函式ui（x，y，z）、vi（x，y，z）、wi（x，y，z）（i=1，2，…，n）疊加而成，即
式中Ai、Bi、Ci為待求係數，共3n個。將u、v、w代入作為泛函的總勢能Π的表達式，根據彈性學最小勢能原理，總勢能變分為零，即有駐值條件：
這是關於3n個待求係數Ai、Bi、Ci的3n個代數方程。解出3n個未知係數便得到全部位移。通過對位移進行微商並利用應力-應變關係就得到應力。由於瑞利-里茲法假設的位移函式u、v、w可以不滿足力的邊界條件，所以位移函式的構成比較容易，計算也比較方便，但有時求出的應力誤差較大。
在振動問題中，如果將物體的可能位移表達為若干給定的位移的線性組合，而以瑞利商（見瑞利原理）作為位移的泛函，則利用瑞利商取駐值時條件，就可求出物體振動的固有頻率的近似值。
套用：
在機械工程領域，它被用於計算多自由度系統（如彈簧-質量系統、變截面軸上的飛輪）大致的共振頻率；還可以計算圓柱體的折斷載荷。瑞利-里茲法是瑞利法的擴展。
以下的討論舉一個最簡單的例子（2個集中彈簧和2個集中質量，並只考慮2個模態振型）。因此M= [m1,m2] 且K= [k1,k2]。
為該系統假設一個由兩項組成的模態振型，其中一個用因數B加權。例如Y= [1, 1] +B[1, –1]。
簡諧運動理論認為撓度等於0時的速率為角頻率ω乘以最大撓度(y)。本例中，每個質量的動能
等等，而每個彈簧的勢能(PE)等於1/2k1Y1^2等等。對於連續系統，該表達式要麻煩得多。因為引入了無阻尼假設，因此整個系統當y=0時的KE等於v=0時的PE。由於不存在阻尼，系統各點同時達到v=0的狀態。
因此，由KE = PE得：
注意模態振型的實際振幅總會從兩邊消去。也就是說，假設撓度的真正數值並不重要。我們在意的是振型。
由於ω與B有關，為了找到最小的ω，我們令dω / dB = 0。此時的B的取值可以使得ω最小。由於振型是假設的，通過該方法得到的ω是需要預測的基頻的上界。我們需要得到的是這個上界的最小值。
該方法有很多技巧，最重要的是試圖找到儘量真實的假設振型。例如在梁的撓曲問題中，使用一個儘量接近真實解得變形模態是明智的。對於大部分簡單的梁連線問題，即使振型的階次很低，一個四次的函式就足夠了。彈簧和質量並不必離散，它們可以使連續的或者是雜糅的。只要能夠描述分散式的KE和PE，或把連續的單元離散，該方法可以很容易編程來找到複雜分散式系統的自然頻率。
該方法可以反覆疊代使用，把附加的模態振型疊加到先前的最佳解上。也可以建立一個用許多參數B和振型組合的長表達式，最後對它們求偏導。
在振動問題中，如果將物體的可能位移表達為若干給定的位移的線性組合，而以瑞利商（見瑞利原理）作為位移的泛函，則利用瑞利商取駐值的條件，就可求出物體振動的固有頻率的近似值。
