基本介紹
- 中文名:閔科夫斯基泛函
- 外文名:Minkowski functional gauge
- 適用範圍:數理科學
簡介

性質
泛函
拓撲線性空間

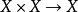
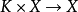

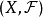


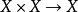
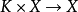

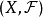
閔科夫斯基泛函是拓撲線性空間上的一類非負值函式,是研究凸集的有效工具。...... 閔科夫斯基泛函是拓撲線性空間上的一類非負值函式,是研究凸集的有效工具。...
,XU是商空間(X,PU(·))/{x|PU(x)=0},而XV是商空間(X,PV(·))/{x|PV(x)=0}的完備化空間,PU(·)及PV(·)是由U和V各自產生的閔科夫斯基泛函...
零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數.反之,設{pλ|λ∈Λ}是E上一族半範數,E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸的...
零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數.反之,設{pλ|λ∈Λ}是E上一族半範數,E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸的...
零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數。反之,設{pλ|λ∈Λ}是E上一族半範數,E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸...
零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數。反之,設{pλ|λ∈Λ}是E上一族半範數,E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸...
零元的每個均衡凸鄰域V的閔科夫斯基泛函 pv(x) 是E上的連續半範數。反之,設 是E上一族半範數,E上使 均為連續的最弱拓撲是局部凸的,且零元的均衡凸鄰域...
零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數。反之,設{pλ|λ∈Λ}是E上一族半範數,E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸...
零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數.反之,設{pλ|λ∈Λ}是E上一族半範數,E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸的...
零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數。反之,設{pλ|λ∈Λ}是E上一族半範數,E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸...
