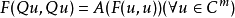第一類西格爾域

給定正整數n和非負整數m，記V為n維實歐氏空間Rⁿ中以原點為頂點的開凸錐，又設V不包含整條直線，則Cⁿ中的域D(V)={z∈Cⁿ|Imz∈V}稱為錐V上第一類西格爾域。

基本介紹

• 中文名：第一類西格爾域
• 外文名：Siegel domain of first kind
• 適用範圍：數理科學

簡介

給定正整數n和非負整數m，記V為n維實歐氏空間Rⁿ中以原點為頂點的開凸錐，又設V不包含整條直線，則Cⁿ中的域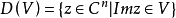稱為錐V上第一類西格爾域。

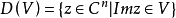
第二類西格爾域

設H₁,H₂,...,H_n，均為m(m>0)階埃爾米特方陣，u∈C^m為m×1復矩陣，為u的轉置共扼矩陣，令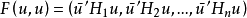

若存在n個m階埃爾米特方陣H₁,H₂,...,H_n，使對任意u∈C^m，均有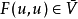，其中為V的閉包，且F(u,u)=0若且唯若u=0，則C中的域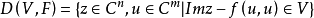

稱為第二類西格爾域。

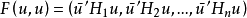
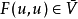
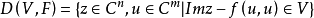
第一類西格爾域和第二類西格爾域這兩類西格爾域統稱為西格爾域。

性質

記A為n階實非奇異方陣，R上線性變換σ:y=Ax稱為關於V不變，如果σ(V)=V，所有使V不變的可逆線性變換構成的集合，記為Aff(V)。

如果在Aff(V)中存在V上可遞李變換群G_v，且任取σ∈G_v，記為y=Ax，則存在m階非奇異複方陣Q，使得C上有非奇異線性變換τ:u→Qu，且，這時西格爾域D(V,F)必線性可遞，稱為齊性西格爾域，它全純同構於齊性有界域。反之，齊性有界域全純同構於齊性西格爾域。