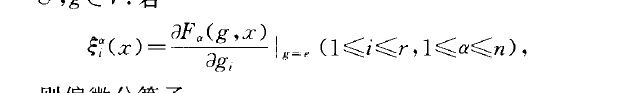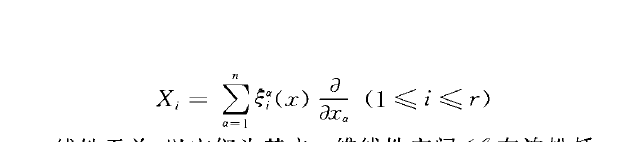李變換群(Lie transformation group)一種特殊的李群.指流形上某些變換構成的李群.
相關詞條
- 李變換群
李變換群(Lie transformation group)一種特殊的李群.指流形上某些變換構成的李群...... 李變換群(Lie transformation group)一種特殊的李群.指流形上某些變換構成的...
- 無限群
挪威數學家S.李在1883年關於連續群的文章中引進了無限連續群,他藉助於一種微分方程來定義這種群,所得的變換並不依賴於有限多個連續的參量,而是依賴於任意函式,...
- 通用覆蓋群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。李群是由挪威數學家S.李創立的一類連續變換群。1870年前後,S.李開始...
- 外爾群
1 概念 2 群 3 代數群 4 變換群 5 半單李代數 6 嘉當李代數 外爾群概念 編輯 外爾群(Weyl group)是作用在根繫上的一種變換群。設L為復半單李代數,...