基本介紹
- 中文名:通用覆蓋群
- 外文名:universal covering group
- 領域:代數
- 性質:李群
- 相關人物:挪威數學家S.李
- 定義:相關於給定李群的一種李群
概念介紹,群,李群,連通,覆蓋群,
概念介紹
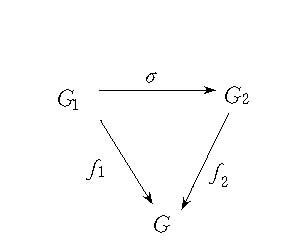
通用覆蓋群是指相關於給定李群的一種李群。設G和G1為連通李群。若存在G1到G上之同態映射f,使任取g∈G,f(g)為G中離散子集;且任取g1∈f(g),存在g1在G1中之鄰域U1以及g在G中之鄰域U,使得f:U1→U為到上之同胚,則G1稱為G的覆蓋群,f稱為G1到G上之覆蓋映射。記(G,f)為G之覆蓋群,若J1及J分別為G1及G之李代數,則f的微分df為J1到J上之李代數同構。設G為連通李群,(G1,f1),(G2,f2)為G的覆蓋群。若存在連通李群G1到G2上的同構σ,可得交換圖(右圖),即f2°σ=f1,則稱(G1,f1)和(G2,f2)是等價的。互相等價的覆蓋群的性質完全相同。若給定連通李群G,則在等價意義下惟一存在一個覆蓋群(G^,f^),使得G^為連通且單連通李群,此時稱(G^,f^)為G的通用覆蓋群。因此,若任意給定李代數L,則在群之同構意義下惟一存在一個連通且單連通李群G^,使得G^之李代數和給定的李代數L同構,且任一連通李群G,只要G的李代數和L同構,則必存在G^到G上之覆蓋映射f^,使得(G^,f^)為G之通用覆蓋群,這時同態核f^(e)=Γ^為G^之離散正規子群,所以包含在G^之中心C(G^)中,且連通李群G和商群G^/Γ^同構,Γ^稱為連通李群G之龐加萊(Poincaré,(J.-)H.)群,也就是G的一階同倫群。
 通用覆蓋群
通用覆蓋群群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合,a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”,運算結果稱為“乘積”)滿足:
(1)封閉性,a·b∈G;
(2)結合律,即(a·b)c = a·(b·c);
(3)對G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,則稱G對於所定義的運算“·”構成一個群。例如,所有不等於零的實數,關於通常的乘法構成一個群;時針轉動(關於模12加法),構成一個群。
滿足交換律的群,稱為交換群。
群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱,就存在群。例如,可以用研究圖形在變換群下保持不變的性質,來定義各種幾何學,即利用變換群對幾何學進行分類。可以說,不了解群,就不可能理解現代數學。
李群
李群是由挪威數學家S.李創立的一類連續變換群。
1870年前後,S.李開始研究連續變換群的概念,並用它們闡明微分方程的解,將微分方程進行分類。1874年,他建立了李群的一般理論。一個李群可以表示成如下形式:

李群理論在最初的相當長一段時間內僅與一些微分方程的積分有聯繫,而與數學的其他分支關係不大。在19世紀的最後10年以及20世紀,李群理論在各種不同方向,主要是代數學和拓撲學方面得到了迅速的發展,成為數學的一個重要分支。李群理論的第一個近代化的敘述是由原蘇聯數學家龐特里亞金於1938年給出的。20世紀50年代,李群理論的發展進入了一個新的階段,主要標誌是代數群論的創立。代數幾何方法的套用使李群理論的經典結果得到新的闡述,從而揭示了它與函式論、數論等理論的深刻聯繫。緊接著,p進李群的理論也得到重大發展。事實上,李群理論與數學的幾個主要分支都有聯繫:通過李變換群與幾何學、拓撲學的聯繫,通過線性表示論與分析的聯繫等。李群在物理學和力學中也有著重要套用。
連通
無向圖G中,若點u,v之間存在路,則稱u,v是連通的.若無向圖G的任意二點都是連通的,則G稱為連通圖。
若認為無向圖G的任意點“自身是連通的,則無向圖G中點的連通關係是點集的一個等價關係,即適合自反性、對稱性、傳遞性的關係。於是,G的點集V能劃分成互不相交的子集V1,V2,…,Vk的並;V1∪V2∪…∪Vk=V,i≠j,Vi∩Vj=φ。不同的Vi,Vj,中的點互不連通,而同一Vi中的點彼此連通。每個Vi的點及它們關聯的邊構成G的子圖Gi,稱為G的一個連通分支;W (G) =k稱為G的連通分支數,當W (G)=1時,稱G是連通圖。
無向連通圖的這兩個定義是等價的。
對於有向圖G來說,若存在u到v的有向路,則說u可達v。當然,u可達v時,未必u可達v。有向圖G的任意二點都相互可達時,G稱為強連通的;若G的任意二點,至少有一點可達另一點,則G稱為單側連通的;若G略去邊的方向時是連通圖; 則彌G是弱連通的。強連通圖必是單側連通圖;單側連通圖必是弱連通圖。其逆均不真。
