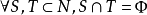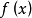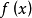凸對策(convex game)是一類有特殊贏得函式的對策,如果對於局中人Ⅰ的任意純策略x∈X,贏得函式A(x,y)是y的一個凸函式,稱此對策G為凸對策。
基本介紹
- 中文名:凸對策
- 外文名:convex game
- 所屬學科:數學
- 所屬問題:運籌學(對策論)
- 相關概念:凸函式,完全構型等
基本概念,凸對策的性質,
基本概念
設 為局中人集,
為局中人集,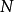 上對策全體仍記為
上對策全體仍記為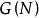 或
或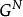 ,
,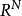 (或
(或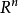 )為
)為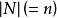 維歐幾里德空間。
維歐幾里德空間。

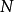
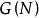
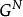
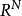
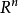
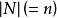
任給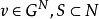 ,定義
,定義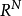 中超平面
中超平面
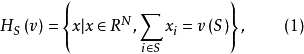

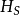
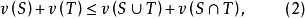

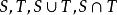

凸對策的性質
下面介紹凸對策的一些性質。
性質1對固定的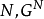 上所有凸對策全體形成凸錐(convex cone)。
上所有凸對策全體形成凸錐(convex cone)。
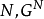
性質2 設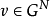 ,則
,則 是凸對策的充要條件為:
是凸對策的充要條件為:
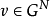

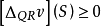
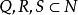
性質3凸對策在策略等價意義下不變,即若 是凸對策,而
是凸對策,而 和
和 策略等價,則
策略等價,則 也是凸對策。
也是凸對策。




性質4 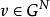 ,則下列條件等價
,則下列條件等價
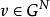
(i)  是凸對策;
是凸對策;

(ii)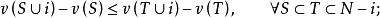
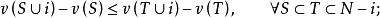
(iii)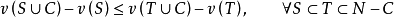 。
。
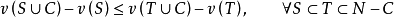
給定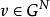 ,由於核心C是凸多面體,為了刻畫凸對策解的結構,我們引進一些概念。
,由於核心C是凸多面體,為了刻畫凸對策解的結構,我們引進一些概念。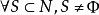 ,記
,記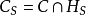 ,顯然
,顯然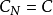 ,為方便起見,記
,為方便起見,記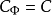 。
。
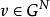
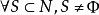
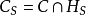
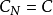
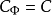
定義1 給定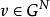 ,如果對
,如果對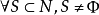 ,則稱核心構形(core configuration)
,則稱核心構形(core configuration) 為完全構形(complete configuration)。
為完全構形(complete configuration)。
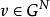
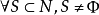

定義2 給定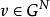 ,如果核心構形
,如果核心構形 滿足
滿足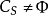 ,且
,且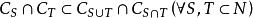 成立,則稱
成立,則稱 為有規則(regular)構形。
為有規則(regular)構形。
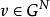

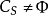
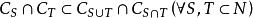

性質5 設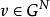 為凸對策,則
為凸對策,則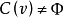 。
。
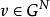
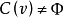
推論設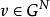 ,則
,則 是凸對策的充要條件是對
是凸對策的充要條件是對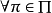 ,有
,有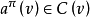 。
。
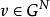

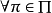
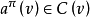
引理7設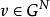 ,
, 為有規則構形,則對任何遞增序列
為有規則構形,則對任何遞增序列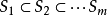 ,
,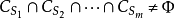 。特別地,當
。特別地,當 ,有規則構形為完全構形。
,有規則構形為完全構形。
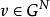

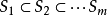
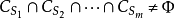

性質6 給定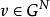 ,
, 是凸對策的充要條件是核心構形
是凸對策的充要條件是核心構形 是有規則構形。
是有規則構形。
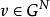


下面將轉向凸對策的核的研究。如果 是0-單調對策,則
是0-單調對策,則 的核
的核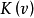 與準核
與準核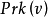 相等,即
相等,即


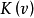
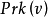
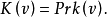
性質7設v是凸對策,則
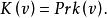
性質8設 是凸對策,於是
是凸對策,於是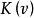 只包含一個點。
只包含一個點。

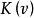
因此,如果 是一凸對策,核、準核以及核子三者都是重合的,可用求字典序的方法來求出凸對策的核。
是一凸對策,核、準核以及核子三者都是重合的,可用求字典序的方法來求出凸對策的核。