基本介紹
- 中文名：凸多面體
- 外文名：convex polyhedron
- 別稱：歐拉多面體
- 學科：數學
- 截面：凸多邊形
- 釋義：每一面所決定的平面的同一側
簡介,歐拉定理,性質,凸n頂體及其性質,
簡介
由若干個平面多邊形圍成的空間圖形叫做多面體，圍成多面體的各個多邊形叫做多面體的面，兩個面的公共邊叫做多面體的棱，棱和棱的公共點叫做多面體的頂點，連線不在同一面上的兩個頂點的線段叫做多面體的對角線。
凸多面體，也稱歐拉多面體，是一種簡單多面體，即整個多面體都在其任何一個面所在平面同側的多面體。凸多面體的任何一個面延展都不會通過它的內部，即把凸多面體的任何一個面伸展成平面，它的所有其他各面都在這個平面的同側。凸多面體內部或界面上任何兩點所連的線段都在凸多面體內或界面上。一個多面體是凸多面體的充分必要條件是它的每個多面角是凸多面角。凸多面體是簡單多面體，不是凸多面體的簡單多面體稱凹多面體。凸多面體的任何截面都是凸多邊形，與凹多面體相反。
歐拉定理
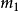
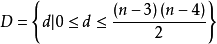
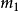
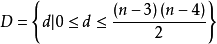
由若干平面多邊形所圈成的封閉的立體叫做多面體，這些平面多邊形稱為多面體的面，這些多邊形的邊和頂點分別稱為多面體的棱和頂點。如果多面體在它們每一面所決定的平面的同一側，剛稱此多面體為凸多面體，一個凸多面體的表面可連續地變形為一個球面，則稱之為簡單多面體。
設G是一個簡單多面體，頂點數為V，棱數為E，面數為F，則有著名的歐拉定理：
性質
凸多面體的主要性質有：
（1）凸多面體的面必為凸多邊形；
（2）凸多面體的多面角必為凸多面角；
（3）直線與凸多面體的面的交點，最多只有兩個(直線段在多面體的面內的情形除外)。
凸n頂體及其性質
定義：若一個凸多面體有n個頂點，則稱該多面體為凸n頂體，簡稱為n頂體。
對於n頂體，有如下一些性質：
（1）如果n頂體中每個面均為三角形，則這個n頂體中棱的條數，面的個數，對角線的條數均為定值，且棱數
，面數
，對角線條數
。
（2）任意n頂體的面角之和均相等，為n邊形內角和的2倍，即2(n- 2)180°。
（3）在所有的n頂體中，每個面均為三角形的n頂體是存在的，而且它的棱數、面數與對角線數均為最多。當n頂體的面不全是三角形時，有結論（4）。
（4）如果一個n頂體有
個四邊形面，
個五邊形面，
個六邊形面，… ，
個(k+ 3)邊形面，其餘面均為三角形面，則該多面體共有
條棱，有
個面，有
條對角線。
（5）任意n頂體的面數m，棱數l，對角線數d均在下列範圍的整數之內：
（6）任意n頂體的面數m，棱數l，有且只有下列範圍之內的整數個：
（7）任意一個n頂體，有且只有d條對角線，其中：
。
