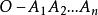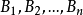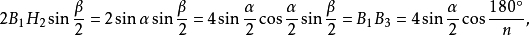凸多面角(convex polyhedral angle)一種多面角，把多面體的任何一個面伸展為平面，如果所有其他各面都在這個平面的同側，這樣的多面體叫做凸多面體。
凸多面體其它的等價定義：
(1)如果多面體內部任意兩點連結的線段都在這個多面體的內部，這樣的多面體叫做凸多面體。
(2)如果多面體的所有對角線都在這個多面體的內部，這樣的多面體叫做凸多面體。
基本介紹
- 中文名：凸多面角
- 外文名：convex polyhedral angle
- 所屬學科：幾何學
- 對應名詞：凹多面角
- 別稱：立體角
基本概念,性質定理,定理1,定理2,定理3,定理4,推論1,定理5,定理6,定理7,例題解析,
基本概念
多面角(polyhedral angle)又稱“立體角”，過平面外一點O向平面內的簡單多邊形的頂點引射線，所有相鄰射線所夾的平面部分圍成的立體圖形，稱為多面角。點O稱為多面角的“頂點”，射線稱為“棱”，相鄰兩棱所夾的角稱為“面角”，相鄰兩棱所夾的平面部分稱為“側面”，多面角按照它的側面數目分別稱為三面角、四面角等等。如果所給的多邊形是凸的，則相應多面角稱為凸多面角；否則稱為凹多面角。凸多面角的面角和小於四個直角，多面角每相鄰兩個面間的二面角稱為多面角的二面角，凸多面角各二面角之和大於(
)直角，而小於
直角(
表示棱數)。
圖1兩個多面角的各面角對應相等，並且各二面角也對應相等，則稱這兩個多面角為全等多面角，各面角相等，並且各二面角也相等的凸多面角稱為正多面角。
性質定理
定理1
凸n面角各面角的平面角之和小於360°。
定理2
凸n面角各二面角的平面角之和大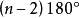於
且小於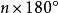
。
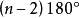
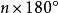
證明 如圖2，設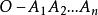
是凸n面角，在其內部作一射線OP，則把凸n面角 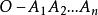分割成n個三面角
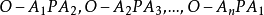，設凸n面角 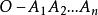的二面角的平面角之和是S，由相關定理得
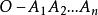
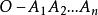
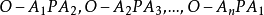
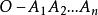
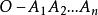
圖2定理3
凸多面角的其中一個面角小於其餘面角的和。
證明 設這個凸多面角是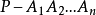
，則
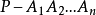
定理4
n(n是整數，n≥3)個角滿足這些角的和小於360°且任意一角小於其他角的和，則以這些角為面角能構成凸n面角的面角。
推論1
給定凸n(n是整數，n≥4)面角的各個面角，則滿足條件的凸n面角有無數種。
由定理3及定理4立即得定理5。
定理5
n(n是整數，n≥3)個角能構成凸n面角的面角的充要條件是這些角的和小於360°且任意一角小於其他角的和。
定理6
那么點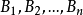
共面，並且多邊形
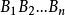是正n邊形；
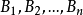
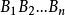
並且正n邊形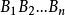的中心與點O的連線垂直於平面
。
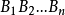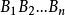
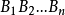
定理7
如果兩個正多面角的棱數和面角都相等，那么這兩個正多面角全等。
例題解析
正n面角的面角等於
，二面角等於
，求與的關係。
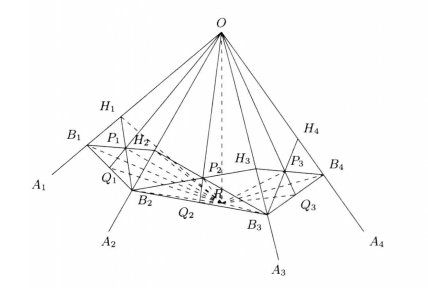圖3解：如圖3，從正多面角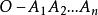的各棱截取n點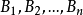，使
，則
