基本介紹
- 中文名:正多面角
- 外文名:regular polyhedral angle
- 所屬學科:數學(立體幾何)
- 簡介:面角、二面角都相等的凸多面角
- 性質:一種特殊的多面角
基本概念,相關介紹,
基本概念
多面角(polyhedral angle)又稱“立體角”。過平面外一點O向平面內的簡單多邊形的頂點引射線.所有相鄰射線所夾的平面部分圍成的立體圖形,稱為多面角。點O稱為多面角的“頂點”,射線稱為“棱”,相鄰兩棱所夾的角稱為“面角”,相鄰兩棱所夾的平面部分稱為“側面”,多面角按照它的側面數目分別稱為三面角、四面角等等。如果所給的多邊形是凸的,則相應多面角稱為凸多面角,否則稱為凹多面角。凸多面角的面角和小於四個直角,多面角每相鄰兩個面間的二面角稱為多面角的二面角。凸多面角各二面角之和大於(2n-4)直角,而小於2n直角(n表示棱數)。
若多面角的面角都相等,二面角也都相等,就稱為正多面角(regalar polyhedral angle),兩個面數相同的正多面角,它們既是對稱多面角又是全等多面角。
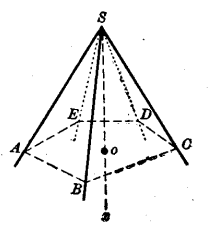 圖1
圖1相關介紹
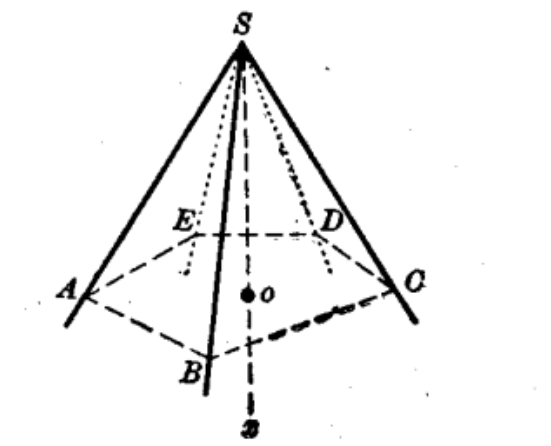
所謂正多面角是指一個凸多面角S-ABCDE (圖1),它的各面角相等,並且各二面角相等(凸多面角指類似於星狀正多邊形有星狀的正多面角)。
所謂球面正多邊形是指一個球面凸多邊形,它的各邊相等且各角相等。顯而易見,對於頂點在一個球心的正多面角,在球上對應著一個球面正多邊形,並且反過來也成立。
在一個正多面角S-ABCDE中,三面角S-ABC,S-BCD,S-CDE,...是全等的,因為有相等的二面角夾於分別相等的面角之間,且有同向。
但有一個旋轉存在將棱SA帶到SB上,並將棱SB帶到SC上(因為∠ASB=∠BSC),三面角S-ABC於是取S-BCD的位置,所以SC來到SD上。仿此,SD來到SE上;等等。因此,有一個旋轉存在將正多面角變換為其自身,每一面取下一面的位置。推廣言之,有一個旋轉存在將正多面角變換為其自身,每一面取其後p個的位置:顯然只須重複上面的旋轉p次就行了。
第一個旋轉的角顯然以圓周的n分之一為度量,n表示多面角的面數,因為當我們重複這旋轉n次後,多面角就旋轉了一周重合於自身上。
這樣一個旋轉(把它重複n次相當於旋轉一周)稱為n階的(*我們有時也把一個旋轉稱為n階的,把它重複n次相當於旋轉了若干周。但必須指出,當周數與n不互質時,這旋轉的階數是小於n的)。當一個圖形經過某一2、3、..階旋轉而沒有改變(*這裡是指位置而不是外形沒有改變),就稱為它以這旋轉軸作為2、3、...階的軸。
如果p是n的一個因數,當我們把上面提到的旋轉重複到p次,就得出另外一個旋轉,它的角以圓周的n'分之一為度量,其中,n'代表整數n/p。
因此可看出,一個圖形的n階軸也是這圖形的n'階軸,n'表示n的任一因數。
凡2階軸(因之,由上面所述,凡偶階軸)是的反射軸(奇階軸則不如此)。
多面角的n階軸顯然和所有的棱形成等角:它是這多面角外接迴轉錐的軸。
因此又得出,一個球面正多邊形可內接於一圓,它的頂點顯然將這圓分成相等的部分(*仿此可證明,一個球面正多邊形可外切於一圓):這就是在繞Sx的旋轉中,它的一個頂點所畫的平行圓。換句話說,如果在正多面角S-ABCDE各棱上,取等長SA = SB= SC= SD=SE,那么這些長度的末端是一個正多邊形的頂點,它的平面垂直於Sx而且中心o在Sx上,因此我們照這樣構成了一個正稜錐。
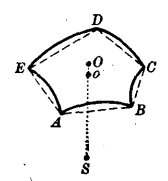 圖2
圖2直線So顯然在這多面角內:通過點o延長,它便截以S為中心以SA為半徑的球於一點O(圖2),這點在球面多邊形ABCDE內部,稱為這多邊形的極。它事實上是多邊形外接圓的兩極之一,即在這圓內的那一個(因∠ASO為銳角)。
反之,在一個正稜錐頂點的多面角,容許一些旋轉,換句話說,有一些旋轉存在把它變換為其自身,即那些把錐底變換為其自身的旋轉。另一方面,如果一個多面角容許一個旋轉,在這個旋轉中每一面取下一面的位置,它便可看作為在一個正稜錐頂點的多面角,而且它是正多面角,因為每一面等於下一面,而且每一二面角等於下一二面角。
最後,由於正多邊形都具有在它平面上的對稱軸,所以凡正稜錐,因之凡正多面角,都具有通過以上說過的一些旋轉的軸So的對稱平面。