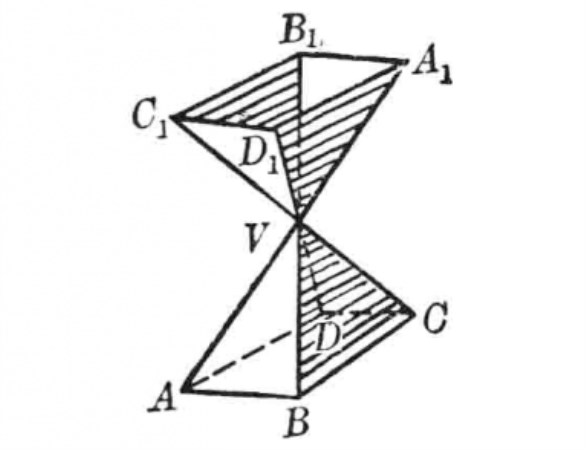
對頂多面角(vertically opposite polyhedral angles)是兩個特殊相關的多面角,指具有公共頂點且關於頂點成中心對稱的兩個多面角,它們反向相等。將一個多面角的每一條棱過它的頂點反向延長,組成另一個多面角,這兩個多面角稱為對頂多面角,它是具有特殊位置關係的對稱多面角。
基本介紹
- 中文名:對頂多面角
- 外文名:vertically opposite polyhedral angles
- 所屬學科:數學
- 所屬問題:立體幾何(多面角)
- 簡介:有公共頂點且關於頂點成中心對稱
定義,相關介紹,
定義
如果將一個多面角的每一條棱過它的頂點延長,就組成了另一個多面角,這兩個多面角叫做對頂多面角。如圖1中,將多面角V-ABCD的各棱過它的頂點V延長,組成多面角V-A1B1C1D1,這樣,多面角V-ABCD和多面角V-A1B1C1D1叫做對頂多面角。
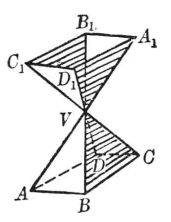 圖1
圖1很顯然, 這兩個對頂多面角的面角AVB、BVC、...、DVA和A1VB1、B1V1C1、...、D1VA1是分別相等,且它們的二面角VA、VB、... 、VD和VA1、VB1、.. VD1也分別相等。
如果將多面角V-A1B1C1D1轉動,使棱VA1同著VA相合,則多面角V-ABCD的各個棱VA、VB、VC...排列的順序是成反時針方向,而多面角V-A1B1C1D1的各個棱VA1、VB1、VC1...排列的順序是成順時針方向。
相關介紹
如果兩個面數相同的多面角,它們對應的面角和二面角分別相等,但排列的順序相反,這兩個多面角,叫做對稱多面角。
 圖2
圖2顯然,對頂多面角是具有特殊位置關係的對稱多面角。
如圖2中,多面角V-ABC和多面角V-A1B1C1是對稱多面角,MN是∠CVA1的平分線,如果把多面角V-A1B1C1繞著MN為軸翻轉一個平角,則棱VA1和VC相重合,棱VC1和VA相重合,且兩個面角A1VC1和AVC相重合。
但是二面角VA1不一定等於二面角VC,因此二面角VA1也就不一定能和二面角VC重合,所以平面A1VB1也不一定和平面CVB重合。同樣地兩個平面C1VB1和AVB也不一定重合,因而棱VB1可以落到另一個位置如VB2,但和VB不相重合。
可知:兩個多面角V-ABC和V-A1B1C1,雖然它們是成對稱,但它們的對應部分卻不一定都處處重合,也就是這兩個多面角不一定是全等的。
關於這一點,我們可以想像到常用的手套,可以把兩隻手套排成對稱形,但是如果要把它的一隻套在另一隻上面,由於手心、手背以及五個指頭的順序不同,是不可能的。
只有兩個面數相同的正多面角,它們既是成對稱(即鏡照相等),又是全等的。所以我們又得到定理:兩個對稱多面角是成鏡照相等,但不一定全等。