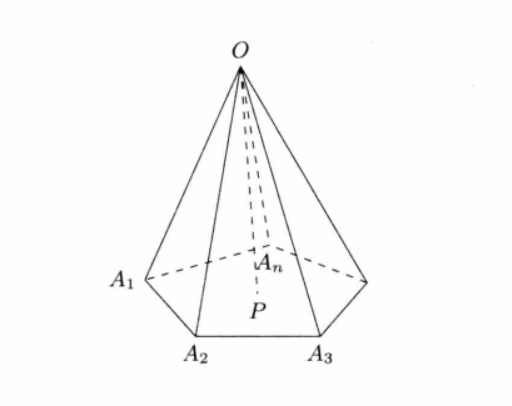
多面角的任何兩個面不相交，任何棱不在它的面內且每棱只能作為兩個面角的邊，這樣的多面角叫做簡單多面角(simple polyhedral angle)。不是簡單多面角的多面角叫做復多面角，有時也叫做星形多面角。
基本介紹
- 中文名：簡單多面角
- 外文名：simple polyhedral angle
- 所屬學科：數學
- 所屬問題：立體幾何（多面角）
- 舉例：凸多面角
基本介紹,相關性質,多面角的性質定理,多面角的二面角和定理,
基本介紹
簡單多面角是一種多面角，指滿足下列條件的多面角：
1.多面角的任意兩個面角的內部無公共點；
2.多面角的任何一條棱不在多面角的一個面角的內部；
3.多面角的任兩條棱不重合。
簡單多面角把空間分成兩個部分，如果將簡單多面角的頂點放在球心，則各面與球面的交線是球面上一些大圓劣弧首尾相接的封閉球面折線，且把球面分成兩個不同的部分。不是簡單多面角的多面角稱為複雜多面角或星形多面角。
假若就多面角每面所在平面來說，其餘各面都在同一半面內(在同側)便叫它做凸多面角。
凡凸多面角一定是簡單多面角，而簡單多面角未必是凸多面角。凸多面角的性質：(1)三面角的任意兩個面角的和大於第三個面角；(2)凸多面角所有面角的和小於四個直角。
相關性質
多面角的性質定理
凸多面角所有面角的和小於四直角。如圖1中，凸n面角V-A1B1C1...E1。以一個平面截這多面角的n條棱和n個面，得到凸n邊形ABC...E，把多邊形的每個頂點A、B、C、...、E都看作某一個三面角的頂點，根據三面角性質定理有：
∠EAB<∠VAE+∠VAB；
∠ABC<∠VBA+∠VBC；
∠BCD<∠VCB+∠VCD；
......
∠DEA<∠VED+∠VEA。
圖1把這些同向不等式的兩邊分別相加，左邊和仍小於右邊之和。但左邊的和就是n邊形ABC..E的所有內角之和等於(n-2)×180°。右邊的和是從n個三角形VAB、VBC、......等的內角和中減去多面角的所有面角的和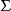
所余的差等於n×180°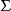－。因此可以得到n×180°－360°< n×180°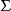－，所以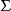<360°。
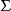
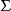
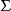
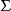
多面角的二面角和定理
n面角的n個二面角的和大於(n－2)×180°。
如圖2，已知n面角S-ABCD....K，求證(二面角SA+二面角SB+二面角SC+...+二面角SK)>(n-2)×180°。
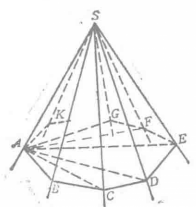圖2簡證如下：作一平面截多面角各棱，則截面為一個n邊形ABC...K，在n邊形ABC...K內，自A作多邊形的對角線AC、AD、...，把n邊形分成為(n-2)個三角形。
過這些對角線及多面角頂點分別作平面SAC、SAD、...，將n面角分成(n-2)個三面角。這些三面角的所有二面角的和等於n面角所有二面角的和。
由於任何三面角的三個二面角的和大於180°，所以(n- 2)個三面角的二面角的和就大於(n-2)×180°。
