仿射擬陣

仿射擬陣(affine matroid)是一種組合構形，它是與矩陣擬陣類似的擬陣M(E)，不同的是，這裡的E是仿射空間A中的有限點構成的集合，而且在A中沒有真子仿射空間可以包含E，仿射擬陣M(E)的獨立集依次為單點集、兩點構成的線段、三點構成的三角形、四點構成的四面體、多點組成的單純形，其單純形上秩函式之值為構成單純形的點數，仿射擬陣的平集，是有關點集的仿射包與E的交集，而它的基則是張成E的單純形。

基本介紹

• 中文名：仿射擬陣
• 外文名：affine matroid
• 所屬學科：數學（組合序）
• 簡介：一種組合構形

基本介紹

定義1 記F=GF(q)是q個元素的有限域，V(n，q)為GF(q)上的n維線性空間，把V(n，q)中的全體qⁿ個向量看作是一個n×qⁿ矩陣A的列向量，我們就得到了一個域F上的向量擬陣M_GF(q)[A]，這個擬陣通常也記作V(n，q)。

設{v₁，v₂，…，v_m}是V(n，F)的一個可重複子集合。若m>0，且存在不全為零的數量a₁，a₂，…，a_m∈F滿足

和

則稱{v₁，v₂，…，v_m}是在F上仿射相關的(affinely dependent)，若{v₁，v₂，…，v_m}不是仿射相關的，則稱{v₁，v₂，…，v_m}是在F上仿射無關的(affinely independent)。

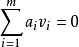
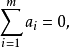
定義2設{v₁，v₂，…，v_m}⊆V(n，F)是一個可重複的向量集，又設E是{v₁，v₂，…，v_m}的標號集合。定義

={ 所標記的向量是在F上仿射無關的}，

則 滿足獨立集公理(I1)-(I3)（見下文），從而(E， )是個擬陣，稱為一個仿射擬陣(affine matroid))。

證明 記每個v_i為n維列向量，定義矩陣(其列也為E所標記)

為F上的(n+1)×m矩陣，其中A的第一行的每一個元素都是F的乘法單位元。從仿射相關的定義可知，對每個子集X⊆E， X所標記的向量是在F上仿射相關的充分必要條件是X所標記的A的列向量是在向量空間V(n+1，F)中是線性相關的，因此 滿足獨立集公理(I1)， (I2)和(I3)。

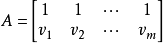
定義3當F是個有限域時，由V(n，F)中全體向量組成的仿射擬陣稱為一個仿射幾何(affine geometry)，記作AG(n，F)。若|F|=q，通常AG(n，F)也記為AG(n，q)。

從定義可知，仿射擬陣一定不含有環，但卻可以有平行元素，因此一個仿射擬陣不一定是個簡單擬陣。

一個擬陣(matroid)M是一個有序對(E， )，其中E且是一個有限集合， ⊆2^E是E中子集的集合，它們滿足以下的公理：

(I1)∅∈ 。

(I2)若I∈ ，及I'⊆I，則I'∈ 。

(I3)若I₁，I₂∈ 且|I₁|<|I₂|，則存在e∈I₂-I₁使得I₁∪e∈ 。

集合 中的元素稱為擬陣M的獨立集(independent set)。因此公理(I1)-(I3)稱為擬陣的獨立集公理。擬陣M通常也記作M=M(E， )，以強調這是一個在E上以 中元素為獨立集的擬陣。

舉例說明

下面考察兩個例子。

(i)記擬陣V(3，2)-{0}為F₇，稱為Fano擬陣。若用向量擬陣的記號，則F₇=M₂[A]，其中

(ii)考慮V(2，R)中向量集合

E={(0，0)，(0，1)，(0，2)，(1，0)，(2，0)，(1，1)}，

(由於E中向量兩兩不同，故可認為這些向量可由它們自己來標號)。記

則在E上的向量擬陣M_R[A₁]與相應的仿射擬陣M_R[A₂]是兩個不同構的擬陣。特別地，仿射擬陣不含有環。