基本介紹
定義,例子,性質,和內部的關係,另請參閱,
定義
作為數學的一個分支,在泛函分析中,向量空間子集的代數內部(英語:Algebraic interior)或徑向核(英語:Radial kernel)是對內部概念的細化。 它是給定集合相對於該點是吸收的的點構成的子集,即集合的徑向點構成的集合。代數內部的元素通常被稱為內點(英語:Internal point)。
正式地,如果X是線性空間,則 的代數內部是
的代數內部是


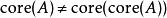
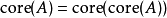
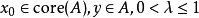

例子
如果 ,則有
,則有 ,但
,但 且
且 。
。




性質
令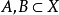 則:
則:
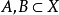
A是吸收的若且唯若




和內部的關係

如果A是非空凸集且X有限維的,則有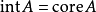
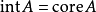
如果A是有非空內部的凸集,則有

如果A是閉凸集且X是完備度量空間,則有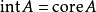
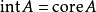
另請參閱
- 擬相對內部
- 有序單位


