基本介紹
形式定義
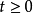





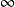


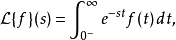

逆變換


性質和定理






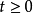







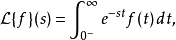








拉普拉斯變換是工程數學中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數實數t(t≥ 0)的函式轉換為一個參數為複數s的函式。拉普拉斯...
拉普拉斯變換法(method of Laplace transform)求解常係數線性常微分方程的一個重要方法。運用拉普拉斯變換將常係數線性常微分方程的求解問題化為線性代數方程或方程組...
雙側拉普拉斯變換(bilateral Laplace transformation)是一種積分變換,作用對象是任意實數t的實數函式或是複變函數 f(t),作用結果是F(s),其形式類似機率中的動差...
拉普拉斯逆變換為當已知信號函式x(t)的拉普拉斯變換X(s),求解信號的時域表達式x(t)。...
數學家、物理學家 主要成就 天體力學 拉普拉斯變換 機率論 代表作品 《天體力學》,《宇宙系統論》 星座 牡羊座 目錄 1 人物生平 2 個人貢獻 3 與拿破崙...
對一個實變數函式作拉普拉斯變換,並在複數域中作各種運算,再將運算結果作拉普拉斯反變換來求得實數域中的相應結果,往往比直接在實數域中求出同樣的結果在計算上...
拉普拉斯變換(英文:Laplace Transform),是工程數學中常用的一種積分變換。...... 拉普拉斯變換(英文:Laplace Transform),是工程數學中常用的一種積分變換。...
拉普拉斯在研究天體問題的過程中,創造和發展了許多數學的方法,以他的名字命名的[4] 拉普拉斯變換、拉普拉斯定理和拉普拉斯方程,在科學技術的各個領域有著廣泛的套用。...
拉普拉斯變換是工程數學中常用的一種積分變換。...... 右端的F(S)是拉普拉斯積分的結果,此積分把時域中的單邊函式f(t)變換為以復頻率S為自變數的復頻域函式F(S...
此外,他還是分析機率論的創始人,因此可以說拉普拉斯是套用數學的先驅。 在研究天體問題的過程中,他創造和發展了許多數學的方法,以他的名字命名的拉普拉斯變換、...
拉普拉斯妖(Démon de Laplace)是由法國數學家皮埃爾-西蒙·拉普拉斯於1814年提出的一種科學假設 [1] 。此“惡魔”知道宇宙中每個原子確切的位置和動量,能夠使用...
▪ 拉普拉斯變換 ▪ 小波變換 數學變換方法概念 編輯 數學變換方法是更格策略反映到數學思維中的一種方法。指在研究和解決數學課題時,採取迂迴的手段達到目的的...
拉普拉斯1749年3月23日生於法國諾曼第,1827年3月5日卒於巴黎。法國著名數學家和天文學家,拉普拉斯是天體力學的主要奠基人,是天體演化學的創立者之一,是分析機率論...
用變換方法,把解微分方程的問題變換為解代數方程的問題,從而轉化為較初等的數學運算.現代數學中許多變換問題已成了專門的研究課題,例如拉普拉斯變換、傅立葉變換等....
積分變換無論在數學理論或其套用中都是一種非常有用的工具。最重要的積分變換有傅立葉變換、拉普拉斯變換。由於不同套用的需要,還有其他一些積分變換,其中套用較為...
人們利用拉普拉斯變換。將微分方程變換成代數方程,可以簡化運算和求解,由於拉氏變換是將時間域變為頻率域,因此人們把這種系統描述的方法稱之為頻域法。[1] ...
分離係數法可以求解有界空間中的定解問題,分離變數法可以求解無界空間的定解問題;也可以用拉普拉斯變換法去求解一維空間的數學物理方程的定解。對方程實行拉普拉斯...
在 [4] 電路分析中要求解任意激勵的零狀態回響時,可採用卷積積分法和拉普拉斯變換法,現分別敘述如下:(1)卷積積分法已知電路的衝激回響為h(t),則任意激勵e(t...
