一般來說,一個函式的傅立葉級數既含有正弦項,又含有餘弦項。特別地,只含有正弦項的傅立葉級數稱為正弦級數,只含有餘弦項的傅立葉級數稱為餘弦級數。
基本介紹
- 中文名:正弦級數和餘弦級數
- 外文名:sinusoidal functon and cosine function
- 性質:兩種特殊的傅立葉級數
- 套用學科:數學
以2l為周期的函式的傅立葉級數




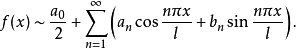



正弦級數與餘弦級數
奇函式的傅立葉級數—正弦函式


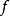



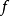


偶函式的傅立葉級數—餘弦級數

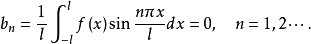

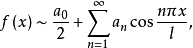
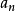




套用








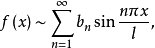









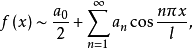

一般來說,一個函式的傅立葉級數既含有正弦項,又含有餘弦項。特別地,只含有正弦項的傅立葉級數稱為正弦級數,只含有餘弦項的傅立葉級數稱為餘弦級數。




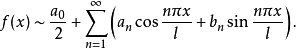





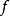



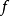



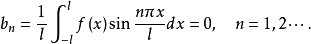

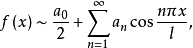
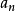












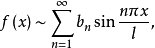









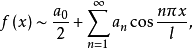

一般來說,一個函式的傅立葉級數既含有正弦項,又含有餘弦項。特別地,只含有正弦項的傅立葉級數稱為正弦級數,只含有餘弦項的傅立葉級數稱為餘弦級數。...
法國數學家傅立葉發現,任何周期函式都可以用正弦函式和餘弦函式構成的無窮級數來表示(選擇正弦函式與餘弦函式作為基函式是因為它們是正交的),後世稱傅立葉級數為一...
由於用正弦級數和餘弦級數這兩個函式系表達層間剪應力和層間正應力,而且在分析過程中未作任何忽略;同時,又因為所涉及的級數都可以求和,故所得到的層間應力解都是...
習題1-21.3 正弦級數和餘弦級數習題1-31.4 周期為2l的周期函式的傅立葉級數習題1-41.5 傅立葉級數的複數形式習題1-5第二章 傅立葉變換2.1 傅立葉積分...
8.7.2 Fourier級數8.7.3 Dirichlet收斂定理8.7.4 正弦級數和餘弦級數習題8.78.8 任意區間上的Fourier級數8.8.1 區間的Fourier級數...
9.1.2 函式的傅立葉級數展開習題9-19.2 正弦級數和餘弦級數習題9-29.3 一般周期函式的傅立葉級數9.3.1 周期為2l的周期函式的傅立葉級數...
11.4 函式展成冪級數及其套用 11.5 傅立葉級數 11.6正弦級數和餘弦級數 11.7 周期為2l的周期函式的傅立葉級數第12章 微分方程 12.1 基本概念 12.2 可分...
12.7 正弦級數和餘弦級數 .. 89總習題 12 .. 91答案.. 101參考資料 1. 高等數學(II)跟蹤習題冊(下) .清華大學出版社[引用日期2018-04-12] ...
9.4.3 函式的冪級數展開式的套用 習題9.4 9.5 傅立葉級數 9.5.1 以2π為周期的函式展開成傅立葉級數 9.5.2 正弦級數和餘弦級數 9.5.3 以...
第四章 Fourier級數和Sturm.Liouville理論§4.1 正交性和Fourier級數定義§4.2 Four-ier級數收斂定理§4.3 正弦級數和餘弦級數及其套用...
7.5.2 周期為27c的函式展開成傅立葉級數7.5.3 正弦級數和餘弦級數7.5.4 任意區間上的函式展開為傅立葉級數習題7.5第8章 線性代數初步8.1 行列式的定義...
預賽按照數學類專業與非數學類專業分別評獎,設一至三等獎,統一頒發“全國大學生數學競賽(一、二、三)等級獎”證書;決賽評獎等級按絕對分數評獎,頒發“全國大學生...
11.了解傅立葉級數的概念和狄利克雷收斂定理,會將定義在 上的函式展開為傅立葉級數,會將定義在 上的函式展開為正弦級數與餘弦級數,會寫出傅立葉級數的和函式的...
