基本介紹
- 中文名:維塔利覆蓋引理
- 外文名:Vitali covering lemma
- 領域:數學
引理敘述,證明,討論,套用,參見,
引理敘述
有限多球




無限多球







證明
有限情形
取這一族球中半徑最大的一個球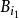 ,然後除去所有與
,然後除去所有與 相交的球。再從剩下的球中取半徑最大的為
相交的球。再從剩下的球中取半徑最大的為 ,如此類推。那么任何其他的球必定因為和某個
,如此類推。那么任何其他的球必定因為和某個 相交而被除去,這個球的半徑不大於
相交而被除去,這個球的半徑不大於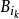 ,因此包含在
,因此包含在 之內。
之內。
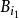



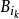

無限情形
設已取 ,k為某大於1的整數。設
,k為某大於1的整數。設 是
是 中不與
中不與 中任何球相交的全部球的子集。取
中任何球相交的全部球的子集。取 為
為 內互不相交球的子集之中的極大者。
內互不相交球的子集之中的極大者。






設 。任何其他的球B必在某一個
。任何其他的球B必在某一個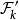 中,因此這個球與
中,因此這個球與 中一個球
中一個球 相交,而
相交,而 的半徑大於B的半徑的二分之一,故此B包含在
的半徑大於B的半徑的二分之一,故此B包含在 之內。
之內。

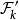




討論
因為有無限多球時,可能不存在半徑最大的球,所以在構造中,每一步選擇的球的半徑,只要求接近餘下的球的半徑的上確界。而結果中的5並非最佳常數。將 的定義中的
的定義中的 的2換成任何大於1的數c,那么就可把結果中的5換成1+2c,即可以用任何大於3的數取代。不過由於未必有半徑最大的球,以致不能像有限多球時用3取代,以下是一個簡單例子。
的2換成任何大於1的數c,那么就可把結果中的5換成1+2c,即可以用任何大於3的數取代。不過由於未必有半徑最大的球,以致不能像有限多球時用3取代,以下是一個簡單例子。


在平面 中,給出如下的一族球:對每個正整數n,
中,給出如下的一族球:對每個正整數n, 是半徑為
是半徑為 的閉球,若n為奇數,
的閉球,若n為奇數, 的圓心在
的圓心在 ;若n為偶數,則圓心在
;若n為偶數,則圓心在 。所有球都包含原點(0,0),故任意兩個球都相交,因此包含互不相交的球的子集只能有一個球。這一族球的半徑上確界是2,然而全部球的半徑都小於2。若選任何一個
。所有球都包含原點(0,0),故任意兩個球都相交,因此包含互不相交的球的子集只能有一個球。這一族球的半徑上確界是2,然而全部球的半徑都小於2。若選任何一個 為這個子集,因有半徑更大的球
為這個子集,因有半徑更大的球 在原點的另一側,故此
在原點的另一側,故此 不覆蓋
不覆蓋 。
。










套用
這條引理可用於證明哈代-李特爾伍德極大不等式。