基本介紹
- 中文名:貝西科維奇覆蓋定理
- 學科:數學
定理敘述,證明,參見,
定理敘述

而A為當中的球的中心組成的集合。那么F中存在子集 ,每個
,每個 是可數多個互不相交的球的集合,而且
是可數多個互不相交的球的集合,而且




證明
先假設A是有界集合。依次選取球 ,選擇
,選擇 為
為 ,適合條件
,適合條件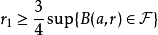 。
。



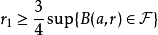
若已選取 。令
。令 。若
。若 ,就停止;若否,選擇
,就停止;若否,選擇 為Bj,適合條件
為Bj,適合條件 。
。





球 Bi有以下性質:
(1)以Bi的選取方法可知,若j>i,則 。
。

(2)將全部球Bi的半徑縮至三分之一,從以上不等式,可證這些縮小的球 互不相交。
互不相交。

(3)若有可數無限多球Bi,因A有界,及縮小的球不交的性質,所以球Bi的半徑趨向0。
(4) 。若Bi數目有限,則結果明顯;若數目是無限多,假如有
。若Bi數目有限,則結果明顯;若數目是無限多,假如有 ,那么F中有球B(a,r),而從上一性質知,對足夠大的j,有
,那么F中有球B(a,r),而從上一性質知,對足夠大的j,有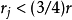 ,與Bj的選取條件矛盾。
,與Bj的選取條件矛盾。


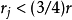
對k> 1,估算Bk和多少個之前選擇的球Bi相交。先將這樣的Bi按半徑ri分成兩組: 為第一組,
為第一組, 為第二組。
為第二組。


對第一組的球 ,將其縮小成
,將其縮小成 後包含在
後包含在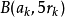 中。
中。 之間互不相交,故總體積不超過
之間互不相交,故總體積不超過 的體積。又因
的體積。又因 ,因此
,因此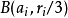 相對
相對 的比例有一個下限,而這下限僅由維數n決定。所以第一組的球的數目有一個僅依賴於n的上限。
的比例有一個下限,而這下限僅由維數n決定。所以第一組的球的數目有一個僅依賴於n的上限。


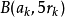



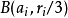

對第二組的球,任取其中兩個球 。考慮以
。考慮以 作頂點的三角形。因Bi,Bj都和Bk相交,又ak不在
作頂點的三角形。因Bi,Bj都和Bk相交,又ak不在 之內,故有不等式
之內,故有不等式



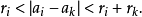


將第二組各個的球的中心和ak之間連成直線,則任意兩條直線之間在ak的夾角不小於arccos(61/64)。ak為中心的單位球面上,這些直線中任何兩條和球面的交點,其間的球面距離,等於直線間的夾角。直線間的夾角下限,就是交點間的球面距離下限。在單位球面上所能容納的這樣的點的數目,有一個只依賴維數n的上限,這也就是第二組球的數目上限。
Bk和之前的球相交的數目上限,是以上兩組的上限的和,於是這個上限只依賴於維數n。這個上限加1設為Mn。現在從 B1開始依次把球放到子集Gi內。輪到Bk時,因為之前的球中最多有Mn-1個和Bk相交,因此在Mn個子集Gi中,必定有至少一個所包含的球都不和Bk相交,於是可以把Bk加進這個子集。這樣就得出了子集Gi,滿足條件















