下極限函式是為判斷函式下半連續性而引進的一個概念。設f(x)是定義在點集E上的擴充實值函式,若在閉包E內的點x的δ鄰域與E的交內,函式f所取的值的下確界為m(x),則m(x,δ)在δ趨於0時的極限稱為f(x)沿E的下極限函式。
基本介紹
- 中文名:下極限函式
- 外文名:lower limit function
- 適用範圍:數理科學
簡介
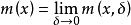
性質
下確界
上極限函式
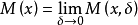
下極限函式是為判斷函式下半連續性而引進的一個概念。設f(x)是定義在點集E上的擴充實值函式,若在閉包E內的點x的δ鄰域與E的交內,函式f所取的值的下確界為m(x),則m(x,δ)在δ趨於0時的極限稱為f(x)沿E的下極限函式。
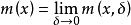
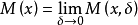
下極限函式是為判斷函式下半連續性而引進的一個概念。設f(x)是定義在點集E上的擴充實值函式,若在閉包E內的點x的δ鄰域與E的交內,函式f所取的值的下確界...
極限函式是高等數學中最基本的概念之一,它是判定函式列一致收斂的一個重要條件...... 極限函式是高等數學中最基本的概念之一,它是判定函式列一致收斂的一個重要條...
函式極限是高等數學最基本的概念之一,導數等概念都是在函式極限的定義上完成的。函式極限性質的合理運用。常用的函式極限的性質有函式極限的唯一性、局部有界性、保...
在數學領域序理論中,經常談論保持特定極限也就是特定上確界或下確界的函式。粗略的說,這些函式把一個集合的上確界/下確界映射到這個集合的像的上確界/下確界...
,使得當 滿足不等式 時,對應的函式值 滿足不等式 ,那么常數 就叫做函式 當 時的極限,或稱函式 收斂於 .記為 或用邏輯符號可以表示為:當 時,有或者...
極限值就是一個函式,當它的自變數趨於無窮,或者某個點時(可以不是該函式定義域裡的點),存在極限,這個極限的值便簡稱為極限值。...
多元實變函式f(p)=f(x1,x2,...,xm ),當它的所有變數同時取極限時函式值的極限,這種極限稱為重極限。當自變數x1,x2,...,xm不是同時取極限,而是依一定...
施托爾茨極限定理是給出求極限的一種方法的命題。施托爾茨極限定理對函式極限也可得出類似結論。...
極限論有多個指代意義。一是作為微積分的基礎,高等數學研究的主要內容是函式的微積分,微積分是研究函式的行為、性質和套用的數學學科,它的基本內容為:極限論、...
S極限(S-limit )在S拓撲下的極限.設函式.f (x)定義在D上,DCT,取值在S中,T,S均是度量空間,p是D的S閉包中的一個點,稱“S中的點、是當二趨於p時f(x...
在測度論中,法圖引理說明了一個函式列的下極限的積分(在勒貝格意義上)和其積分的下極限的不等關係。法圖引理的名稱來源於法國數學家皮埃爾·法圖(Pierre Fatou),...
在高等數學中,極限是一個重要的概念。 極限可分為數列極限和函式極限,分別定義如下。 lim數列極限 編輯 設{Xn} 為實數列,a 為定數.若對任給的正數 ε,總...
