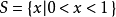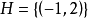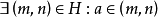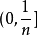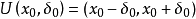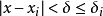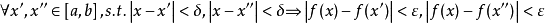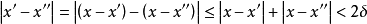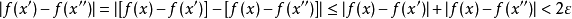有限覆蓋定理：設H是閉區間[a,b]的一個（無限）開覆蓋，則必可以從H中選擇有限個開區間來覆蓋[a,b]。
有限覆蓋定理是一個有用而且重要的定理．它是數學分析處理問題的一種重要方法，在數學各領域中都有廣泛的套用．有限覆蓋定理的作用是從覆蓋閉區間的無限個開區間中能選出有限個開區間也覆蓋這個閉區間．由“無限轉化為有限”是質的變化，它對證明函式的某些性質提供了新的數學方法。
基本介紹
- 中文名：有限覆蓋定理
- 外文名：Heine–Borel theorem
- 又稱：海涅-博雷爾定理
- 分類：數學
- 相關：閉區間
- 屬於：實數定理
簡介,定律定義,推導過程,適用範圍,套用領域,
簡介
有限覆蓋定理：設H是閉區間[a,b]的一個（無限）開覆蓋，則必可以從H中選擇有限個開區間來覆蓋[a,b]。
有限覆蓋定理是一個有用而且重要的定理．它是數學分析處理問題的一種重要方法，在數學各領域中都有廣泛的套用．有限覆蓋定理的作用是從覆蓋閉區間的無限個開區間中能選出有限個開區間也覆蓋這個閉區間．由“無限轉化為有限”是質的變化，它對證明函式的某些性質提供了新的數學方法。
定律定義
在講有限覆蓋定理之前，先介紹覆蓋的概念。
覆蓋：設有任意個區間（可以是開區間，也可以是閉區間，還可以是半開半閉區間；可以是有限個區間，也可以是無限個區間），它們構成了一個集合H（集合H的所有元素均為區間）。如果對於一個數集S，S中的任意一個元素都屬於H中的至少一個區間，那么稱H是S的一個覆蓋。
它的等價定義為，若S包含於任意個區間所構成的並集，則稱這些區間構成的集合H是S的一個覆蓋。
特別地，當H中的元素全部為開區間時，稱H是S的開覆蓋。
例如，數集
，它的一個覆蓋為
。這是因為，對任意0<x<1，必有-1<x<2，即S中的任意一個元素都屬於H，因此H是S的一個覆蓋。
同理，
也是S的一個覆蓋，因為S包含於H'中的元素所構成的並集
。
有限覆蓋定理：設H是閉區間[a,b]的一個（無限）開覆蓋，則必可從H中選擇有限個開區間來覆蓋[a,b]。
推導過程
該定理反應了實數的完備性，可以用戴德金定理來證明。
設閉區間[a,b]有一個無限開覆蓋H，下面結合反證法證明[a,b]能被H中的有限個開區間覆蓋。
假設[a,b]不能被H中的有限個開區間覆蓋，在開區間(a,b)上找一個數x，使閉區間[a,x]被H中的有限個開區間覆蓋。這樣的x一定存在，∵[a,b]被H覆蓋，∴
。那么，在區間(a,n)內任取一個數為x（且該x落在(a,b)上），則有m<a<x<n，即閉區間[a,x]被開區間(m,n)覆蓋。
令所有這些x，連同區間(-∞,a]上的所有數構成一個數集A，並把A在實數集R中的補集設為B。則：
①由取法可知A、B皆非空；
②A∪B=R；
③根據取法，A中的數都落在區間(-∞,x]上（且[a,x]可以被H的有限個開區間覆蓋），而B中的數落在(x,+∞)上（且[x,b]不能被H的有限個開區間覆蓋），∴A中任意一個元素都小於B中任意一個元素。
根據戴德金定理，存在唯一實數η，使η是A、B的分界點，且η要么是A中最大值，要么是B中最小值。
假設η是A中的最大值，顯然有η∈(a,b)。那么，
∵[a,η]被H中有限個開區間覆蓋（並設這有限個開區間構成的集合為H1，H1⊂H）
∴
取足夠小的ε>0，使η+ε仍落在區間(p,q)內，這樣一來，[a,η+ε]依然可以被H1所覆蓋。而H1是H的有限個開區間構成的集合，即[a,η+ε]被H的有限個開區間所覆蓋。
∴η+ε∈A，與η是A中最大值相矛盾。
若η是B中的最小值，η∈(p2,q2)∈H,取足夠小的ε>0，使η-ε仍大於p2，則η-ε∈A。
∴[a,η-ε]被H中有限個開區間覆蓋（並設這有限個開區間構成的集合為H2，H2⊂H）。在H2中加上區間(p2,q2), 形成集合H3，那么H3仍是H中有限個開區間構成的集合。
這樣一來，容易證明[a,η]可以被H3所覆蓋。而H2是H的有限個開區間構成的集合，即[a,η]被H的有限個開區間所覆蓋。
∴η∈A，與η是B中最小值相矛盾。
∴一開始的假設不成立，[a,b]必然被H中的有限個開區間覆蓋，定理得證。
適用範圍
有限覆蓋定理必須注意兩個條件。
一是被覆蓋的區間必須是閉區間，開區間或半開半閉區間不成立。例如對區間
來說，
是其一個無限開覆蓋。但顯然，無論n取值為多少，區間
上依然有 的無窮多個數，因此不能從H中選擇有限個區間來覆蓋 。
二是用來覆蓋閉區間的必須是開區間，閉區間或半開半閉區間不成立。例如對區間
來說，
（n=1,2,3,……）是其一個無限覆蓋，顯然也找不出有限個子區間來覆蓋 。
套用領域
有限覆蓋定理是實數定理，還有確界存在定理；單調有界定理；閉區間套定理；聚點定理；柯西收斂準則的逆否命題。這6個定理是等價的，可以互相推出對方，它們都反應了實數的連續性與完備性，在數學分析上有著重要的運用。
尤其是有限覆蓋定理，它可以推廣到n維空間（此時定理的描述會發生改變，但本質不變），從而定義了緊集和緊空間等。
已知：f(x)在閉區間[a,b]上有定義，且f(x)連續。求證：f(x)在閉區間[a,b]上一致連續。
證明：
∵f(x)在[a,b]上連續
∴對任意x0∈[a,b]，
上式中的δ0(ε,x0)表示δ是ε和x0的函式，而
即意味著
。
固定ε，只讓x0在區間[a,b]上變化，則一般來說δ0也要發生變化。當x0取遍[a,b]上的所有實數時，[a,b]將被所有x0的鄰域
構成的集合S覆蓋，或者說S是[a,b]的一個無限開覆蓋。
由有限覆蓋定理得S中有有限個開區間能覆蓋住[a,b]，不妨設這有限個開區間構成的集合為
。
令
（∵i為有限正整數，∴δi為有限個，在這有限個δi之中一定有最小值），這個δ不再與x0有關，是因為無論對[a,b]上的哪個數xi，當
時，總有
。下證對任意x'和x''∈[a,b]，當|x'-x''|<δ時，總有|f(x')-f(x'')|<ε。
事實上，由連續的定義，
那么，當
時，有
顯然，ε是任意正數，那么2ε也是任意正數，也相應地存在正數2δ。這就證明了f(x)在[a,b]上一致連續。
