基本介紹
- 中文名:確界原理
- 外文名:supremum and infimum principle
- 提出者:波爾查諾(Bolzano,B.)
- 提出時間:1817年
- 套用學科:數學
- 適用領域範圍:實數完備性
定義
上界和下界
上確界和下確界

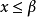






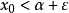

描述
證明




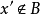





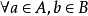


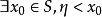



推廣的確界原理
套用














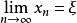
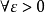




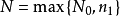



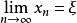
確界存在定理一般指本詞條

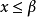






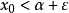





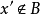





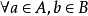


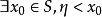

















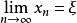
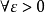




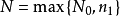



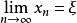
而若存在實數m, ,有 ,則稱m是S的一個下界。顯然,所有大於M的數都是S的...由戴德金定理證明非空有上界數集必有上確界,非空有下界數集必有下確界同理...
閉區間套定理 證明:不妨設 ,f(b)>0.令E={x|f(x)≤0,x∈[a,b]}.由f(a)<0知E≠Φ,且b為E的一個上界,於是根據確界存在原理,存在...
有限覆蓋定理是實數定理,還有確界存在定理;單調有界定理;閉區間套定理;聚點定理;柯西收斂準則的逆否命題。這6個定理是等價的,可以互相推出對方,它們都反應了實數的...
實數連續性定理包括:確界存在性定理,單調有界收斂定理,閉區間套定理,有限覆蓋定理,聚點定理,波爾查諾——魏爾斯特拉斯定理、柯西準則。 這七個定理可由確界存在...
但這裡有一個很微妙的問題,即與連續性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂...
實數系的基本定理也稱實數系的完備性定理、實數系的連續性定理,這些定理分別是確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和...
3.1 確界的概念和確界存在定理3.2 閉區間套定理3.3 凝聚定理3.4 Cauchy收斂準則3.5 覆蓋定理3.6 數列的上極限和下極限3.7 對於教學的建議...
1.2 實數集的完備性與確界存在定理 1.3 映射與函式的概念 1.4 複合映射與複合函式 1.5 逆映射與反函式 1.6 初等函式與雙曲函式 習題1.1 第二節 數列的極限...
3.1 確界的概念和確界存在定理3.1.1 基本內容(67)3.1.2 例題(67)3.1.3 練習題(69)3.2 閉區間套定理3.2.1 基本內容(70)3.2.2 例題(71)3.2.3 ...
