基本介紹
- 中文名:聚點定理
- 外文名:Bolzano–Weierstrass theorem
- 別稱:波爾查諾-維爾斯特拉斯定理
- 表達式:若S為非空無限點集,則S必有聚點。
- 提出者:波爾查諾
- 提出時間:1817年
- 套用學科:數學
- 適用領域範圍:數學分析
定律定義
聚點
聚點定理
推導過程
聚點定理
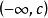
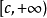
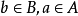
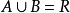
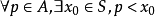
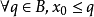
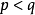
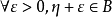







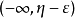


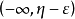


緻密性定理






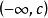
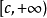
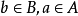
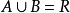
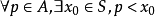
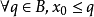
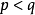
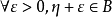







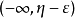


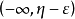








聚點定理,也稱為維爾斯特拉斯聚點定理,定量內容是:實軸上的任一有界無限點集S至少有一個聚點。該定理的一般形式(又叫緻密性定理,波爾查諾-維爾斯特拉斯定理)...
聚點原理(accumulative point principle)亦稱外爾斯特拉斯定理,或波爾查諾-外爾斯特拉斯定理,刻畫實數系R的連續性的常用命題之一。它斷言:R(Rn或度量空間)的每個有界...
聚點是拓撲空間的基本概念之一。設A為拓撲空間X的子集,a∈X,若a的任意鄰域都含有異於a的A中的點,則稱a是A的聚點。集合A的所有聚點的集合稱為A的導集,...
波爾查諾-維爾斯特拉斯定理是指有界數列必有收斂子列。從極限點的角度來敘述緻密性定理,就是:有界數列必有極限點。...
區間套定理與單調有界定理、數列的緻密性定理和柯西收斂準則、聚點定理、有限覆蓋定理共同構成實數集完備性的基本定理,並且這六個定理是相互等價的,對於研究實數集的...
有限覆蓋定理:設H是閉區間[a,b]的一個(無限)開覆蓋,則必可以從H中選擇有限個開區間來覆蓋[a,b]。有限覆蓋定理是一個有用而且重要的定理.它是數學分析處理...
實數連續性定理包括:確界存在性定理,單調有界收斂定理,閉區間套定理,有限覆蓋定理,聚點定理,波爾查諾——魏爾斯特拉斯定理、柯西準則。 這七個定理可由確界存在...
但這裡有一個很微妙的問題,即與完備性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂...
所以從點集的角度來描述該定理,則是:有界點集至少有一個聚點(即聚點定理)。參考資料 1. 《數學辭海》編輯委員會.數學辭海 第三卷 : 中國科學技術出版社,2002...
實數系的基本定理也稱實數系的完備性定理、實數系的連續性定理,這些定理分別是確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和...
6.2.1 區間套定理 6.2.2 有限覆蓋定理 6.2.3 聚點定理 6.2.4 實數集完備性基本定理的等價性 6.3 上極限和下極限簡介 小結 複習題 習題答案或...
第七章 實數的完備性 1 關於實數集完備性的基本定理 一 區間套定理 二 聚點定理與有限覆蓋定理 三 實數完備性基本定理之間的等價性 2 上極限和下極限...
關於實數集完備性的基本定理 一 區間套定理與柯西收斂準則 二 聚點定理與有限覆蓋定理 三 實數完備性基本定理的等價性 2 閉區間上連續函式性質的證明 3 上極限和...
