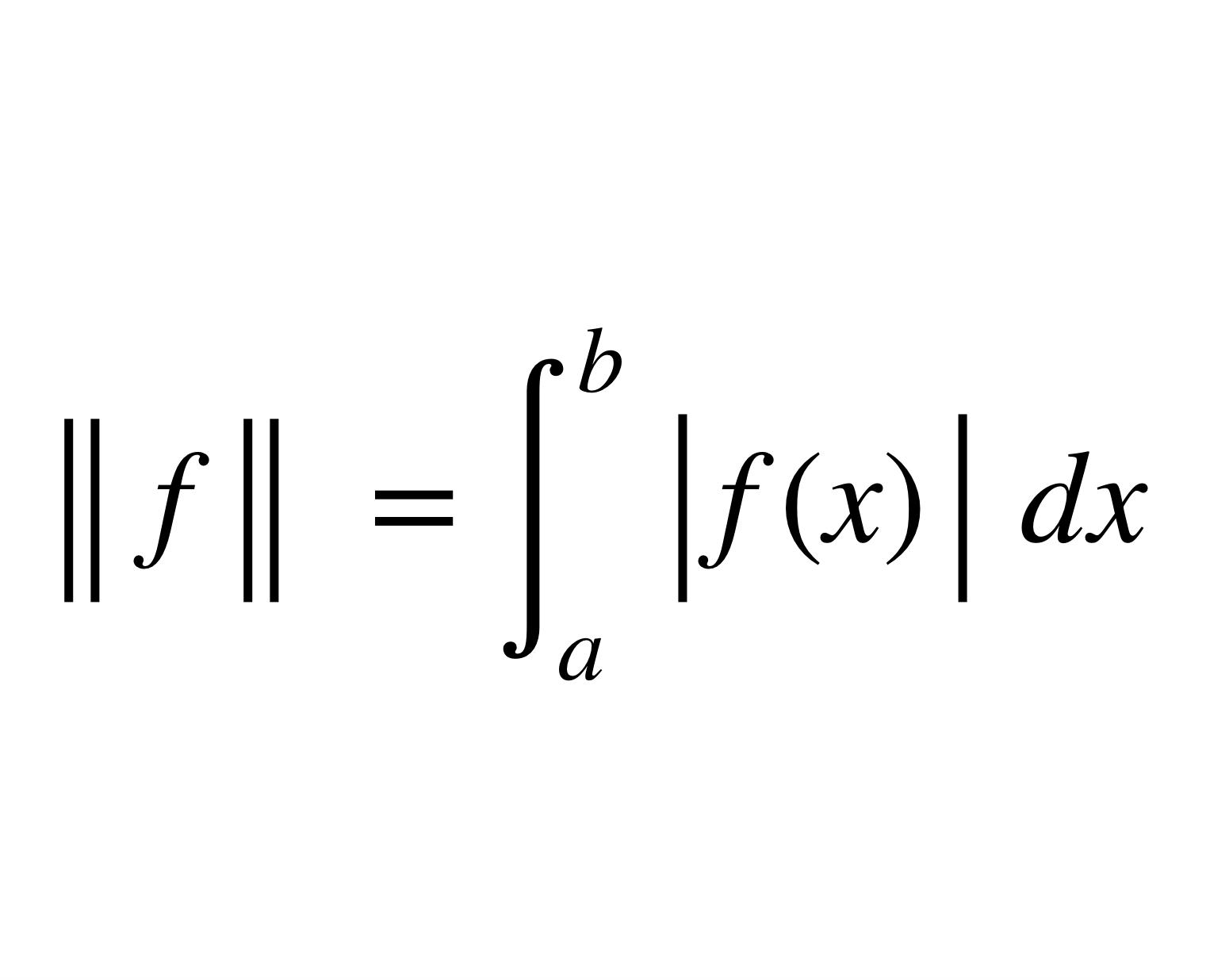平均逼近

平均逼近是在平均收斂意義下的逼近。設F是定義在[a，b]上的某類函式的集合，f：[a，b]→R，若對任意ε>0，存在g∈F，使‖f-g‖₂<ε，則稱f可由F中的函式平均逼近。例如，可積函式可由多項式平均逼近。這個概念可以以明顯的方式推廣到多元函式。

基本介紹

• 中文名：平均逼近
• 外文名：approximation in the mean
• 適用範圍：數理科學

定義

平均逼近指在 範數意義下的逼近，通常考慮在 空間的逼近。對於 的範數定義為

與一致逼近相同，平均逼近的工具通常也採用代數多項式和三角多項式。

關於平均逼近的存在性也有相應的魏爾斯特拉斯定理。

魏爾斯特拉斯定理

波爾查諾-維爾斯特拉斯定理是指有界數列必有收斂子列。從極限點的角度來敘述緻密性定理，就是：有界數列必有極限點。

在數列{x_n}中任意抽取無限多項並保持這些項在原數列中的先後次序，這樣得到的一個數列稱為原數列的子列。根據極限的性質，數列有界是收斂的必要條件，即如果數列收斂，那它一定有界，但反之不一定成立。可是緻密性定理卻告訴我們，只要一個數列有界，那么它一定會有收斂的子數列。

由於子列收斂，設收斂到常數A，根據極限的幾何意義，在A的ε鄰域內總有子列的無數個點。而ε是任意正數，這就意味著在A的任何鄰域內都有子列的無數個點。所以從點集的角度來描述該定理，則是：有界點集至少有一個聚點（即聚點定理）。