疊合度亦稱重合度，是為了討論方程Lx=Nx的解，利用勒雷-紹德爾度來定義的一種度。
基本介紹
- 中文名：疊合度
- 外文名：coincidence degree
- 適用範圍：數理科學
簡介,套用,勒雷-紹德爾度,
簡介
疊合度亦稱重合度，是為了討論方程Lx=Nx的解，利用勒雷-紹德爾度來定義的一種度。
這裡L:domL⊂X→Z是零指標的弗雷德霍姆線性運算元，N:
⊂X→Z是非線性運算元，X,Z是巴拿赫空間，Ω是X中有界開集。由假定可知，存在有限維子空間N0⊂Z與商空間Z/Im L同構，且存在連續投影運算元P:X→ker L,Q:Z→N0滿足ImP= ker L，kerQ= ImL，X= ker L⨁kerP，Z= ImL⨁ImQ。記Kp:ImL→dom L∩ ker P為L在dom L∩ker P上的限制的逆運算元，並令KP,Q=KP(I-Q):Z→domL∩kerP，這裡I為恆同映射。
設J:ImQ→ker L是一同構，並令HJ,P,Q= JQ+Kp,Q:Z→dom L。設N是L緊的（即QN: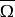
→Z和KP,Q,N:
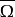→X都是緊的）且0∉F(dom L∩∂Ω)，這裡F= L-N。於是，易知HJ,P,Q=I-A,其中A=P+ JQN+Kp,QN: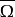→X是全連續運算元，且0∉(I-A)(∂Ω)，故勒雷-紹德爾度deg(I- A,Ω,0)存在，它就定義為F在Ω上關於L的疊合度，記為DL(F,Ω)。
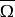
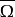
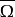
套用
疊合度可證DL(F,Ω)與P,Q以及J（保持定向）的選擇無關，並具有可加性、同倫不變性、可解性等性質。
例如，可解性指的是：若DL(F,Ω)≠0，則Lx=Nx在domL∩|Ω中有解。
疊合度是討論非線性常微分方程邊值問題一個有力工具。
勒雷-紹德爾度
勒雷-紹德爾度是對無窮維賦范線性空間中的全連續向量場建立的拓撲度。
設X是賦范線性空間，Ω是X中的有界開集，F: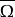
→X全連續，f=I-F是全連續向量場，p∈X\f(∂Ω)，那么，距離dist(p,f(∂Ω))=ε>0。取X的有限維線性子空間Xn與連續映射Fn: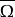→Xn使得p∈Xn，且‖F(x)-Fn(x)‖<ε(∀x∈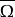)。這時，布勞威爾度deg(
)有意義，且與Xn和Fn的選取無關，把它作為f在Ω上關於點p的拓撲度deg(f,Ω,p)的定義，此即勒雷-紹德爾度。
