弗雷德霍姆線性積分運算元是一類重要的線性積分運算元,是n維空間上的線性運算元當n變成無窮時的極限式。
基本介紹
- 中文名:弗雷德霍姆線性積分運算元
- 外文名:Fredholm linearintegral operators
- 適用範圍:數理科學
簡介
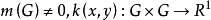
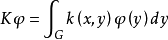
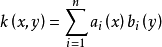
弗雷德霍姆線性積分運算元是一類重要的線性積分運算元,是n維空間上的線性運算元當n變成無窮時的極限式。
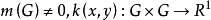
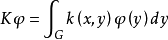
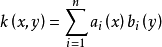
弗雷德霍姆線性積分運算元是一類重要的線性積分運算元,是n維空間上的線性運算元當n變成無窮時的極限式。...
弗雷德霍姆理論是關於線性積分運算元的基本理論之一,是弗雷德霍姆(Fredholm,E.I.)通過積分方程與線性代數方程組類比的方法(即把線性積分方程看成是“無窮維”線性方程...
例如,對泛函分析中平方可積函式、平均收斂、運算元等的形成,對一般線性運算元理論的...D.希爾伯特和E.施密特對第二種弗雷德霍姆積分方程做了重要的工作,特別是關於對稱...
人們從兩種不同的途徑研究非線性問題:①針對具體問題,考察具體非線性運算元的特徵,...此外,對非線性弗雷德霍姆運算元也能定義拓撲度,使之保持許多重要性質。後者在無窮...
20世紀初,在討論第二類線性積分方程時,也得到了和線性方程組完全類似的弗雷德霍姆理論。後來,人們發現這種理論對(線性)全連續運算元也是成立的。...
弗雷德霍姆行列式(Fredholm determinant)是一個由弗雷德霍姆線性積分運算元的核確定的行列式。...
弗雷德霍姆運算元是可逆運算元的推廣。當T是弗雷德霍姆運算元時,對H上的任何緊運算元K,T+K也是弗雷德霍姆運算元。...
非線性積分方程也可以被分成多種類型,例如,弗雷德霍姆型、沃爾泰拉型、哈默斯坦型...如果把積分方程中出現的函式看做是巴拿赫空間X中的元素,把原來的積分運算用運算元...
弗雷德霍姆積分方程的重要推廣和發展,包括允許積分核有不可積的奇點,積分區間是無限區間等多種情形。使弗雷德霍姆定理不成立的線性積分方程,通常稱為奇異積分方程。...
時有無窮多個線性無關解奇異積分方程與弗雷德霍姆積分方程的本質差異在於前者出現在方程中的積分運算元是有界運算元甚至是有逆的,而後者只是相應函式空間中的緊運算元,緊算...
其中未知函式以線性形式出現的,稱為線性積分方程;否則稱為非線性積分方程。積分...的某些邊值問題,引進類似於位勢的積分運算元,往往可歸結為弗雷德霍姆積分方程或...
柯西奇異積分方程(Cauehy singular integral equations)是一類最基本且具有廣泛實際套用的奇異積分方程,其積分是柯西主值意義下的。柯西奇異積分方程與弗雷德霍姆積分...
諾特運算元(Noether operator)亦稱廣義弗雷德霍姆運算元.為了使奇異積分方程理論一般化,將諾特定理成立的運算元稱為諾特運算元,也簡稱中運算元.設X,Y是巴拿赫空間,運算元A:X->Y...
2.2 內積空間中的運算元2.2.1 運算元與伴隨運算元2.2.2 自伴運算元...8.2 線性積分方程的疊代技術8.2.1 弗雷德霍姆線性積分方程8.2.2 沃爾泰拉...
