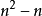厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。
基本介紹
- 中文名:厄米特矩陣
- 外文名:Hermitian Matrix
- 又譯作:埃爾米特矩陣
- 性質:自共軛
定義,性質,推論,
定義
n階複方陣A的對稱單元互為共軛,即A的共軛轉置矩陣等於它本身,則A是厄米特矩陣(Hermitian Matrix)。
例如:矩陣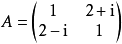 , A就是一個自共軛矩陣。
, A就是一個自共軛矩陣。
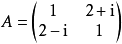
性質
顯然,埃爾米特矩陣主對角線上的元素都是實數的,其特徵值也是實數。對於只包含實數元素的矩陣(實矩陣),如果它是對稱陣,即所有元素關於主對角線對稱,那么它也是埃爾米特矩陣。也就是說,實對稱矩陣是埃爾米特矩陣的特例。
若A和B是埃爾米特矩陣,那么它們的和A+B也是埃爾米特矩陣;而只有在A和B滿足交換性(即AB=BA)時,它們的積才是埃爾米特矩陣。
可逆的埃爾米特矩陣A的逆矩陣A仍然是埃爾米特矩陣。
如果A是埃爾米特矩陣,對於正整數n,  是埃爾米特矩陣。
是埃爾米特矩陣。

方陣C與其共軛轉置的和是埃爾米特矩陣。
任意方陣C都可以用一個埃爾米特矩陣A與一個斜埃爾米特矩陣B的和表示。
埃爾米特矩陣是正規矩陣,因此埃爾米特矩陣可被酉對角化,而且得到的對角陣的元素都是實數。這意味著埃爾米特矩陣的特徵值都是實的,而且不同的特徵值所對應的特徵向量相互正交,因此可以在這些特徵向量中找出一組C的正交基。
如果埃爾米特矩陣的特徵值都是正數,那么這個矩陣是正定矩陣,若它們是非負的,則這個矩陣是半正定矩陣。
推論
(1)n階厄米特矩陣A為正定(半正定)矩陣的充要條件是A的所有特徵值大於(大於等於)0。
(2)若A是n階厄米特矩陣,其特徵值對角陣為V,則存在一個酉矩陣U,使AU=UV。
(3)若A是n階厄米特矩陣,其弗羅伯尼範數的平方等於其所有特徵值的平方和。