基本介紹
- 中文名:廣義特徵值問題
- 外文名:Generalized Eigenvalue Problems
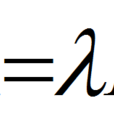
對於形式如下的特徵值問題:求數λ,使方程Ax=λBx有非零解x,這裡A為n階實對稱矩陣,B為n階實對稱正定矩陣,x為n維列向量,則稱該問題為矩陣A相對於矩陣B的...
其中特徵值中存在的複數項,稱為一個“叢(pencil)”。若B可逆,則原關係式可以寫作 ,也即標準的特徵值問題。當B為非可逆矩陣(無法進行逆變換)時,廣義特徵值問題...
對元素為實數或複數的 n×n矩陣A,求數λ和n維非零向量 x使Ax=λx,這樣的問題稱為代數特徵值問題,也稱矩陣特徵值問題,λ和 x分別稱為矩陣A的特徵值和特徵...
這裡的第一種意義不可和下面所說的廣義特徵值問題混淆。特徵向量例如 它只有一個特徵值,也就是λ = 1。其特徵多項式是(λ − 1)2,所以這個特徵值代數重次...
3.4 廣義區間特徵值問題參數頂點求解定理在工程中的套用3.4.1 工程背景3.4.2 尾槳固有振動頻率區間估計3.5 本章結論參考文獻第四章 有阻尼結構系統固有振動頻率...
取駐值,這個駐值就是 。子空間疊代法瑞利一里茲法 用瑞利一里茲法,可以將 階廣義特徵值問題降為一個 階 廣義特徵值問題來求解。記 、 、 、 構成的空間為 ...
第7章 廣義特徵值問題的計算方法7.1 基本方法7.2 廣義特徵值問題的計算方法7.3 廣義特徵值問題的等價形式7.4 其他方法第8章 非線性方程求根...
2.5.3 廣義伽遼金原理2.5.4 加權殘值法2.6 差分法2.7 遷移矩陣法第3章 多自由度系統的振動3.1 無阻尼系統固有頻率3.2 標準特徵值與廣義特徵值問題...
上式為特徵值問題求解器能解決的規範表示。其中,MATLAB LMI工具箱提供的相應的求解器為mincx。3、 廣義特徵值問題(GEVP):已知某線性矩陣不等式約束,解如何最小化...
8.7 一些廣義特徵值問題 411第9章 Lanczos方法 4209.1 方法的導出及收斂性 4209.2 實用Lanczos方法 4289.3 套用於Ax=b和最小二乘 4379.4 Arnoldi方法與非...
第五節 廣義特徵值問題的計算方法一、逆疊代法二、廣義雅可比法三、子空間疊代法第六節 平面剛架動力特性計算程式一、基礎數據檔案及數據格式...
《線性代數計算方法》討論線性代數計算方法的基礎理論和常用算法,內容包括解線性代數方程組地直接法、疊代法、共軛梯度法和線性最小二乘法;求一般n階矩陣特徵值問題...
之所以有如此廣泛的套用,其 主要原因是,LDA(包括其多類推廣)具有以下優點:可以直接求得基於廣義特徵值問題的解析解,從而避免了在一般非線性算法中,如多層感知器,...
1.1 矩陣逆的擾動界限 1.2 線性方程組解的擾動界限 習題 第四章 特徵值問題擾動分析 第五章 廣義特徵值問題擾動分析 第六章 向後擾動分析 參考文獻[2] 參考...
4.6 廣義Jacobi法求解廣義特徵值問題 4.7 Householder變換法 4.8 QL法求解對稱三對角矩陣的特徵值問題 4.9 Sturm序列法求解對稱三對角矩陣的特徵值問題 5 連續系統振...
第四節 廣義特徵值問題習題五第六章 廣義逆矩陣第一節 廣義逆與線性方程組第二節 廣義逆矩陣的定義第三節 廣義逆矩陣的計算與性質...
重特徵值的小參數法 大型汽輪發電機組定子端部繞組的固有振動分析 葉片-盤-軸整體轉子振動特性分析 廣義特徵值問題中重特徵值的特徵向量導數 廣義逆在特徵靈敏度計...
