一個矩陣稱為下三角矩陣如果對角線上方的元素全部為0。類似地,一個矩陣稱為上三角矩陣如果對角線下方的元素全部為0。
定義


- 兩個下三角矩陣的和下三角。
- 兩個下三角矩陣的乘積是下三角。
- 一個可逆的下三角矩陣的逆是下三角。
- 下三角矩陣與常數相乘是一個下三角矩陣。
以上性質對上三角矩陣也成立。
嚴格上(下)三角矩陣
原子三角矩陣


例子

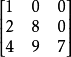
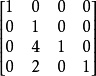

方程組求解




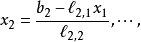

一個矩陣稱為下三角矩陣如果對角線上方的元素全部為0。類似地,一個矩陣稱為上三角矩陣如果對角線下方的元素全部為0。





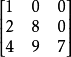
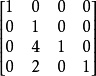





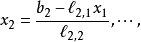

一個矩陣稱為下三角矩陣如果對角線上方的元素全部為0。類似地,一個矩陣稱為上三角矩陣如果對角線下方的元素全部為0。...
三角矩陣是方形矩陣的一種,因其非零係數的排列呈三角形狀而得名。三角矩陣分上三角矩陣和下三角矩陣兩種。上三角矩陣的對角線左下方的係數全部為零,下三角矩陣的...
主對角線以下都是零的方陣稱為上三角矩陣。上三角矩陣具有行列式為對角線元素相乘、上三角矩陣乘以係數後也是上三角矩陣、上三角矩陣間的加減法和乘法運算的結果仍是...
三角形矩陣是一種特殊矩陣,是數域P上主對角線以下或以上的全體元素都是零的n階方陣。...
三角分解法亦稱因子分解法,由消元法演變而來的解線性方程組的一類方法。設方程組的矩陣形式為Ax=b,三角分解法就是將係數矩陣A分解為一個下三角矩陣L和一個上...
準三角形矩陣(quasi-triangular matrix)一種特殊的分塊矩陣.設數域F上的分塊矩陣 若s=t,且當i<j (或i>j時),所有的A_{ij}=0,則稱A為上準三角形矩陣(...
(三角形矩陣)編輯 鎖定 帕斯卡三角形,又稱賈憲三角形、楊輝三角形、海亞姆三角形、巴斯卡三角形,是二項式係數在的一種寫法,形似三角形,在中國首現於南宋楊輝的《...
線上性代數中,三對角矩陣是矩陣的一種,它“幾乎”是一個對角矩陣。準確來說:一個三對角矩陣的非零係數在如下的三條對角線上:主對角線、低對角線、高對角線。...
. 其中L是一個單位下三角矩陣,U是一個單位上三角矩陣,P是一個置換矩陣。 而滿足分解條件的矩陣L,U,P稱為矩陣A的一個LUP分解 [20] 。矩陣...
線上性代數中,塊三對角矩陣是矩陣的一種,它“幾乎”是一個對角矩陣。準確來說:一個塊三對角矩陣的非零係數在如下的三條對角線上:主對角線、低對角線、高對角...
一般來講矩陣範數除了正定性,齊次性和三角不等式之外,還規定其必須滿足相容性:║XY║≤║X║║Y║。所以矩陣範數通常也稱為相容範數。 如果║·║α是相容範數,...
(10) 若B為L矩陣,且bij>=aij, i,j=1,2,...,n,則B的逆存在。(11)存在下三角矩陣T和上三角矩陣U,其中T和U均為L-矩陣,使A=TU....
設M為元素取自交換體K中的n階方陣,把M三角形化,就是確定一個上三角形矩陣T與一個可逆方陣P,使M=PTP-1,設f為典範地對應於M的Kn之自同態,把M三角形化,...
矩陣分解 (decomposition, factorization)是將矩陣拆解為數個矩陣的乘積,可分為三角分解、滿秩分解、QR分解、Jordan分解和SVD(奇異值)分解等,常見的有三種:1)三角...
Cholesky 分解是把一個對稱正定的矩陣表示成一個下三角矩陣L和其轉置的乘積的分解。它要求矩陣的所有特徵值必須大於零,故分解的下三角的對角元也是大於零的。...
需要注意的是,若干個矩陣相乘得到的矩陣的行列式等於這些矩陣的行列式相乘。於是,我們得到: LU=PA 這裡L是一個對角線上元素全為1的下三角矩陣(lower triangular),...
tril是用於matlab中提取矩陣下三角矩陣的函式。...... 用法:tril(X),其中X表示一個矩陣。功能:tril函式是tril(X)產生X矩陣的下三角矩陣,其餘元素補0。...
其中,L為單位下三角矩陣,U為上三角矩陣。 [4] 根據以上定理,可以通過計算矩陣A的所有順序主子式,來判斷矩陣A是否可以進行LU分解,且為唯一分解。...
triu,triu函式是matlab中提取矩陣上三角矩陣的函式。...... 功能:triu函式是matlab中提取矩陣上三角矩陣的函式。triu(X)產生X矩陣的上三角矩陣,其餘元素補0。...
