設M為元素取自交換體K中的n階方陣,把M三角形化,就是確定一個上三角形矩陣T與一個可逆方陣P,使M=PTP-1,設f為典範地對應於M的Kn之自同態,把M三角形化,就是確定Kn的一個基,使在這個基下對應於f的矩陣是上三角形矩陣。
基本介紹
- 中文名:三角形化
- 所屬學科:數學
- 所屬問題:矩陣
- 相關概念:三角矩陣
基本介紹
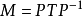

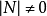
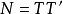



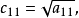
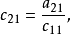
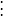
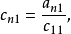
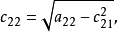

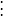
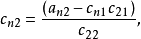
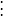

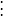
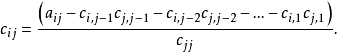
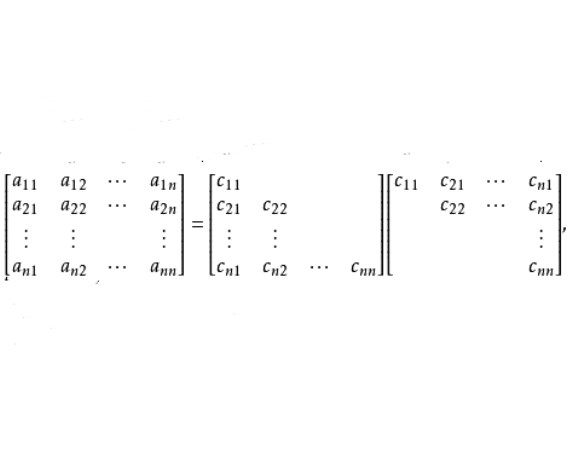
設M為元素取自交換體K中的n階方陣,把M三角形化,就是確定一個上三角形矩陣T與一個可逆方陣P,使M=PTP-1,設f為典範地對應於M的Kn之自同態,把M三角形化,就是確定Kn的一個基,使在這個基下對應於f的矩陣是上三角形矩陣。
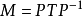

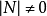
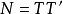



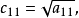
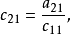
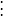
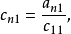
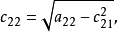

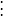
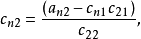

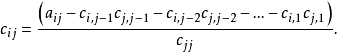
設M為元素取自交換體K中的n階方陣,把M三角形化,就是確定一個上三角形矩陣T與一個可逆方陣P,使M=PTP-1,設f為典範地對應於M的Kn之自同態,把M三角形化,...
在使用OpenGL畫圖的過程中,由於OpenGL不支持直接繪製凹多邊形,所以我們通常需要先將凹多邊形轉化為一組三角形下面就是一個三角化多邊形的算法1) 用單向循環鍊表保存...
三角形定則是指兩個力(或者其他任何矢量)合成,其合力應當為將一個力的起始點移動到另一個力的終止點,合力為從第一個的起點到第二個的終點。...
2月14日,《自然》子刊《Nature Nanotechnology》上刊登了一則讓人不可思議的報導——來自IBM的科學家們造出了一款三角形分子,一償化學家們近70年的夙願。 早在...
魯洛克斯三角形(Reuleaux triangle)又稱“勒洛三角形”、“萊洛三角形”、“圓弧三角形”,是一種特殊三角形,指分別以正三角形的頂點為圓心,以其邊長為半徑作圓弧...
三角化三角形鑲嵌(英語:Triakis triangular tiling)是一種平面鑲嵌,密鋪於歐幾里得平面。...
Delaunay三角化是一種三角剖分DT(P),使得在P中沒有點嚴格處於DT(P)中任意一個三角形外接圓的內部。Delaunay三角化最大化了此三角剖分中三角形的最小角,換句...
三角形法(triangle method)是一種儲量計算法。它的實質是把形狀不規則的礦體,人為地簡化為許多便於計算體積的三稜柱狀體。即在儲量平面圖所圈定的礦體範圍內,以...
三角形行列式(triangular determinant)是一種特殊的行列式,包括上三角形行列式和下三角形行列式,亦稱上三角行列式和下三角行列式,統稱三角形行列式。每個行列式都可以只...
三角形定則是指兩個力(或者其他任何矢量)合成與分解的法則,求其合力應當為將一個力的起始點移動到另一個力的終止點,合力方向為從第一個的起點指向第二個的...
三角形元素(elements of triangle)是三角學的基本概念之一,三角形的三邊(或它們的長度)和三內角(或它們的大小)以及由它們所確定的幾何圖形(或相應的幾何量)統稱...
上升三角形形態上是指多方占優,空方較弱,多方的強大買盤逐步將價格的底部抬高,而空方能量不足,只是在一水平頸線位做抵抗的形式。...
三角形穩定性是指三角形具有穩定性,有著穩固、堅定、耐壓的特點,如埃及金字塔、鋼軌、三角形框架、起重機、三角形吊臂、屋頂、三角形鋼架、鋼架橋都以三角形形狀...
在機率論與統計學中,三角形分布是低限為 a、眾數為 c、上限為 b 的連續機率分布。...... 三角形分布是低限為a、眾數為c、上限為b的連續機率分布 [1] ,...
謝爾賓斯基三角形(英語:Sierpinski triangle)是一種分形,由波蘭數學家謝爾賓斯基在1915年提出。它是自相似集的例子。它的豪斯多夫維是log(3)/log(2) ≈ 1.585。...
萊洛三角形,也譯作勒洛三角形或弧三角形、圓弧三角形,是除了圓形以外,最簡單易懂的勒洛多邊形,一個定寬曲線。其作法為先畫正三角,然後分別以三個頂點為圓心,...
2、最大化最小角特性:在散點集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大。從這個意義上講,Delaunay三角網是“最接近於規則化的“的...
三角形連線簡介 編輯 將三相電源或負載中的每一相的末端與後續相的始端相連,然後再從3個連線點引出端線的連線方式。三角形連線中三相負載的每一相都跨接在兩條...
星形-三角形變換是電路的轉化,可通過基爾霍夫定律來完成,星形電路三相分別為:r1、r2、r3;三角形電路三相分別為:R12、R23、R13。...
三角形的一條邊與另一條邊的延長線組成的角,叫做三角形的外角。外角的個數等於多邊形邊數的兩倍。三角形外角和是360°(多邊形的外角和一般是每個頂點只取一個...
的絕對速度都可以分解為沿轉輪葉片流動的相對速度和隨著轉輪一起旋轉的牽連速度,這三個速度向量構成一個閉合的三角形,一般把這個三角形稱為水輪機水流速度三角形。...
