基本介紹
- 中文名:三角形分布
- 外文名:Triangle distribution
- 學科:機率論與統計學
定義

特例
已知兩點


兩個標準一致變數的分布

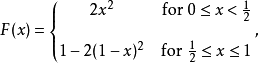

三角形分布的套用
1.商務模擬
2.項目管理
3.工程項目成本風險理論分布
4.風險性成本期望值
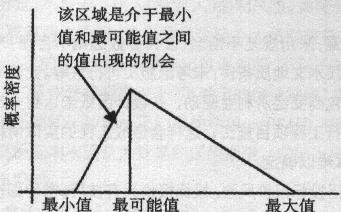 圖1.風險性成本期望值
圖1.風險性成本期望值



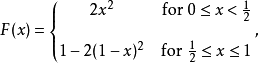

 圖1.風險性成本期望值
圖1.風險性成本期望值在機率論與統計學中,三角形分布是低限為 a、眾數為 c、上限為 b 的連續機率分布。...... 三角形分布是低限為a、眾數為c、上限為b的連續機率分布 [1] ,...
三角分布(triangular distribution),亦稱辛普森分布或三角形分布。在機率論與統計學中,三角形分布是低限為a、眾數為c、上限為b的連續機率分布。...
區位三角形,是指美國社會學家梯利提出的城市社會學分析框架。由地域、人口和活動分別作為三個頂點組成三角形。三角形三邊及三角形整體分別代表不同城市社會學派的...
三角形圖表是一種較特殊的坐標統計圖方法。它是依據等邊三角形中任意點到三條邊的垂直距離之和相等的原理構成三軸統計圖。因此,專用於內部組成為三項結構的數據...
由不在同一直線上的三條線段首尾順次連線所組成的封閉圖形叫做三角形。 平面上三條直線或球面上三條弧線所圍成的圖形,三條直線所圍成的圖形叫平面三角形;三條...
反三角分布(inverse triangular distribution )一種機率分布,其特徵函式 ...... 反三角分布(inverse triangular distribution )一種機率分布,其特徵函式參考資料 1. 數...
三角形矩陣是一種特殊矩陣,是數域P上主對角線以下或以上的全體元素都是零的n階方陣。...
三角形分級法(triangular fractionation)是一種沉澱分級方法。在原始試樣溶液中加入足夠的沉澱劑,使沉澱量為原試樣的一半左右,將沉澱物與清液分離,然後將沉澱物再...
,把總體的所有單位數按組歸併排列,形成各組單位數在總體中的分布,稱統計分布。...洛倫弦曲線與對角線之間的部分A 叫做“不平等面積”,直角三角形OHL的面積(A+B...
設M為元素取自交換體K中的n階方陣,把M三角形化,就是確定一個上三角形矩陣T與一個可逆方陣P,使M=PTP-1,設f為典範地對應於M的Kn之自同態,把M三角形化,...
三角洲又稱河口平原,從平面上看,像三角形,頂部指向上游,底邊為其外緣,所以叫...而成(建造),但波浪或潮汐等作用可以使它們遭受沖刷、改造,並使其重新分布(改造...
德洛內(Delaunay)三角網的定義: 它是一系列相連的但不重疊的三角形的集合, 而且這些三角形的外接圓不包含這個面域的其他任何點。它具有兩個特有的性質:(1) 每個...
三角形主機是由銳角雲團隊所推出的一款基於區塊鏈技術的硬體產品。通過分布式雲存儲、雲計算共享閒置硬碟空間與頻寬獲得數字資產的智慧型硬體。...
帕斯卡分布,負二項分布的正整數形式,描述第n次成功發生在第x次的機率,是統計...他們的研究被認為共同奠定了機率論和組合分析的基礎.在他的《算術三角形》一書...
