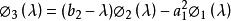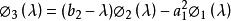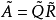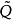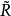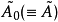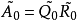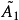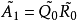基本介紹
- 中文名：塊三對角矩陣
- 外文名：Block three diagonal matrix
- 領域：數學
- 屬性：矩陣
- 元素個數：2n-1
- 相關名詞：三對角矩陣
簡介,定義,塊三對角矩陣的特點,確定塊三對角矩陣的特徵值,QR法,特徵多項式法,
簡介
在線性代數中，塊三對角矩陣是矩陣的一種，它“幾乎”是一個對角矩陣。準確來說：一個塊三對角矩陣的非零係數在如下的三條對角線上：主對角線、低對角線、高對角線。在許多物理問題中，塊三對角矩陣常常作為原始數據出現，因此它們本身是很重要的，這種矩陣僅有（2n-1）個獨立的元素。由塊三對角矩陣確定特徵值由一些較有效的方法，常見的有兩種：QR法、特徵多項式法。
定義
形如
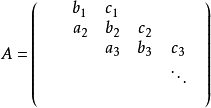
的n×n矩陣A稱為塊三對角矩陣，其中第(i,j)個元素在j>i+1和j<i-1時為零。
塊三對角矩陣的特點
塊三對角矩陣M是一個對角矩陣，若且唯若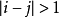
時，有M(i,j)=0。在一個nxn的塊三對角矩陣T中，非0元素排列在如下的三條對角線上：
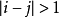
（1）主對角線即i=j；
（2）主對角線之下的對角線（稱低對角線）即i=j+1；
（3）主對角線之上的對角線（稱高對角線）即i=j-1。
這塊三條對角線上的元素總數為3n-2，故可以使用一個擁有3n-2個位置的一維數組來描述T，因為僅需要存儲塊三條對角線上的元素。
確定塊三對角矩陣的特徵值
QR法
一般來說，對於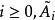
化成
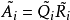，其中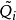
是正交矩陣，
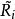是上三角矩陣，則
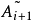被定義為
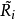和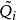
以相反次序乘積式。因為
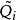是正交矩陣，
。
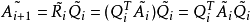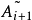是對稱的，與
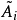有相同的特徵值。我們定義
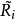和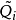
成這樣的形式：
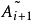是塊三對角矩陣，最終
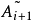趨於變為對角陣，其對角線上的元素給出原矩陣的特徵值。
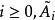
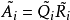
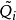
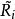
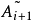
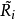
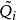
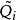
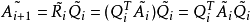
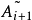
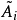
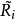
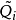
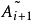
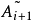
特徵多項式法
特徵多項式法可以像特徵多項式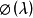
的根一樣確定特徵值。有一種有效的方法來構造塊三對角矩陣的特徵多項式。使用符號法可以求特徵值的歸類，從而形成一個Sturmian序列。然後用對分法或試位法來求精確的特徵值。由Householder變換得到的對稱塊三對角矩陣的特徵多項式為：
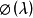
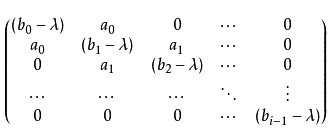
其中，i=1,2,...,n，有：
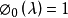
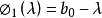
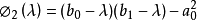
從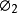
向前的Sturm序列可以表示為：
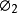
因此有
