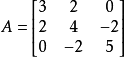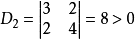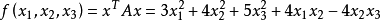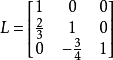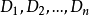順序主子式是取n階方陣的部分元素化為行列式形式。方陣的第k階行列式是由該方陣的前k行和k列元素組成。對於n階方陣A,其共有n階順序主子式。通過計算方陣A的所有順序主子式,可以來判斷一個實二次型是否正定或方陣A是否為正定矩陣,也可以判斷方陣A是否可以進行唯一LU分解。
基本介紹
- 中文名:順序主子式
- 外文名:Sequential Principal Minor
- 本質:由一系列行列式組成
- 特性:n階方陣有n階順序主子式
- 套用1:判定實二次型正定或矩陣正定
- 套用2:判定矩陣是否可唯一LU分解
定義


套用
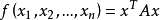
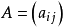

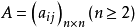
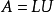
舉例